Determination of Planck's Constant
Contents
Description of the Experiment
The purpose of this experiment is to study the photoelectric effect and calculate Planck's constant using 5 different coloured leds (different wave-lenghts) and a photoelectric cell.
Links
- Video: Soon
- Laboratory: free.elab
- Control room: Planck
- Grade: **
Experimental Apparatus
The photoelectric cell is from the PASCO AP-9368 apparatus. It works like a capacitor where one of the plates emits photoelectrons when excited by light. The potential between the plates of the photocell will increase with the emitted photoelectron accumulation. After reaching a certain voltage, the stopping potential will be greater than the photoelectron's kinetic energy, and these will not have enough energy to reach the second plate. This voltage will depend on the wavelength of the incident light (photon energy).
After each experiment the photocell is connected to ground to discharge.
The leds have different efficiency, leading to different intensities for a chosen brightness. Therefore, the charging time will be different between colors.
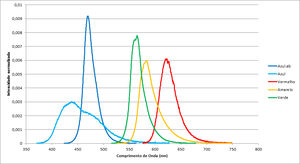
The graph in figure 1 shows each led spectrum, table 1 shows more details.
Please note that the wavelength for each led depends on the junction temperature, and this will depend not only on room temperature, but also on the current passing through the junction. This effect (red shift) is more noticeable in warm-coloured led (green-red) than in the blue one, so the calculation of Planck's constant will suffer a shift.
| Color | Frequency (THz) | Wavelegth (nm) | Espectros dos leds |
|---|---|---|---|
| Blue.ab | 638.7 | 469.70 | File:Espectro Azul.ab.txt |
| Blue | 684.6 | 438.20 | File:Espectro Azul.txt |
| Red | 482.2 | 622.21 | File:Espectro Vermelho.txt |
| Yellow | 514.4 | 583.16 | File:Example.txt |
| Green | 530.8 | 565.22 | File:Espectro Verde.txt |
Protocol
The number of photoelectrons emitted will increase with the intensity of light (corpuscular behaviour of light).
- Choose a led to light upon the photocell
- Measure the stopping potential. Note the time necessary to reach the maximum potential.
- Repeat step 2 for different intensities.
| Color #1 __________(name) | Intensity (%) | Stop Potential (V) | Time (s) |
|---|---|---|---|
| 10% | |||
| ... | |||
| ... | |||
| ... | |||
| ... |
The kinetic energy of the photoelectron depends only on the frequency of the incident light. If the frequency of light increases, the energy will increase.
- Obtain the stop potentials for different colour leds.
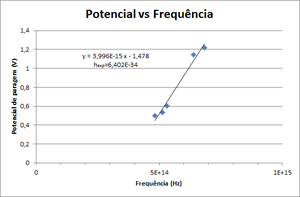
- Draw a graphic of Stop Potential vs Frequency. Fit it to \( V = \frac{h}{e} \nu - \frac{W_0}{e} \) and obtain Planck's constant.
| Colour (name) | Frequency (THz) | Stop Potential (V) |
|---|---|---|
Advanced Protocol
- Study the photocell charging process for different intensities.
- Find the wavelength expected value using the led spectra.
- Use those values for a new graphical fitting and compare the results.
- Redo the voltage vs. frequency graph, this time with error bars.
Note: This setup uses a 12bit ADC from 0V to 5V.
Theoretical Principles
Photoelectric effect
The photoelectric effect happens when a metal surface is illuminated by a light with a given frequency, causing electrons to be freed. When a photon with energy \( E \) collides with a metal, it transfers its energy to an electron in the crystal structure. The emission of electrons is deeply connected to the frequency of the light shone upon the surface. For each metal there is a critical frequency, \( \nu _0 \). If incident radiation has frequency bellow \( \nu _0 \), then there are no emitted electrons. If the former is above the latter, then the kinetic energy of the emitted electrons is proportional to the energy of the photons. The light intensity changes only the number of emitted photoelectrons, not its energy (this goes against what is expected in the classical theory of radiation).
Einstein proposed the following explanation: light is made of photons with a given energy, proportional to frequency (\( \nu \)):
[math] E = h \nu [/math]
Where \( h \) is Planck's constant. The photoelectric effect is, essentially, a collision between a photon (light) and an electron (in the metal) where the former gives all its energy to the latter. Since the electron's energy is higher when in vacuum (as opposed when it's bound to the crystal structure of the metal), the electron is only freed if the photon energy is higher than the difference between the energy of the electron in vacuum and in the metal (figure 1). Thus, the electron leaves the metal with energy equal to the energy of the photon minus the amount "spent" when the electron leaves the metal:
[math] E = h \nu - e \phi [/math]
where \( e \) is the electron charge and \( \phi \) is the diference in workfunction. As the light frequency decreases, the photons have less energy. Bellow a certain critical frequency \( \nu _0 \), no more photoelectrons are emitted. In this case, \( E_{max} = 0 \) and we can write:
[math] h \nu _0 = e \phi \quad or \quad \nu _0 = \frac{e}{h} \phi [/math]
Photoelectric cell
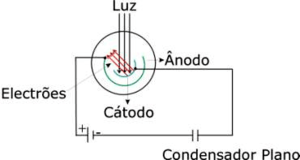
A photoelectric cell is a device where light shines upon a metallic surface (cathode) and excites the electrons that will be collected by a concentric metallic surface (anode), as shown in the figure on the right (it is basically a semi-cylindrical capacitor with very low capacity). If you connect the cathode and anode through an external circuit, you can measure the current created by the photo-electrons. In a more generic sense, the maximum kinetic energy of the electron is determined by applying a stopping potential between the cathode and the anode to prevent electrons from reaching the anode. This way, when current no longer flows, we will know the value of the current.
We begin by applying a voltage to the cell (approximately 9V, because the capacitor is discharged before starting the experiment by short-circuiting the terminals). With the cell in series with the capacitor, the latter will charge as electrons are generated in the cell. This creates an electric current through the cell. As the capacitor charges, the voltage between its terminals increases, reducing the voltage between the terminals of the cell(because \( V_{bat} = V_{Cap} + V_{cell} = constant \)). When the cell voltage reaches \( V_c = \frac{h \nu - e \phi}{e} \), current no longer flows and the capacitor maintains a constant voltage.
Knowing two or more voltage values for certain frequencies, the user can do a linear regression and determine both \( \phi \) and Planck's constant. In the following graphic we can see the relation between the stopping potential V and the light frequency for a given metal. This function is a linear function with slope = \( \frac{h}{\epsilon} \) and y-intercept = \( \phi \).
Historical Elements
In 1921, Albert Einstein won the Nobel Physics Prize for his work on the photoelectric effect.