Difference between revisions of "Determination of Planck's Constant"
| Line 39: | Line 39: | ||
|} | |} | ||
| − | = | + | =Protocol= |
| − | + | The number of photoelectrons emited will increase with the intensity of light. (corpuscular behavior of light) | |
| − | # | + | #Choose a led to light up on the photocell |
| − | # | + | #Measure the stopping potential. Take note the time necessary to reach the maximum potential. |
| − | # | + | #Repit step 2 for diferent intensities. |
{| border="1" style="text-align: center;" | {| border="1" style="text-align: center;" | ||
| − | |+ | + | |+ Exemple of a table |
|- | |- | ||
| − | ! | + | !Color #1 __________(name) |
| − | ! | + | !Intensity (%) |
| − | ! | + | !Stop Potential (V) |
| − | ! | + | !Time (s) |
|- | |- | ||
| | | | ||
| Line 81: | Line 81: | ||
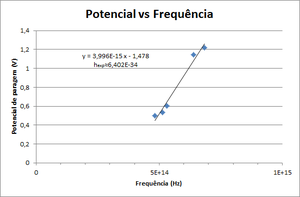
| − | [[File:Constante de Planck.png|thumb|alt=Constante de Planck| | + | [[File:Constante de Planck.png|thumb|alt=Constante de Planck|Figure 2: Potential vs. Peaks Frequency of the spectrum ]] |
| − | + | The photoelectron's kinetic energy depend only on the frequency of light. If the frequency of light increase the energy will increase. | |
| − | # | + | #Obtain the stop potentials for different color leds. |
| − | # | + | #Make a graphic of Stop Potential vs Frequency and obtain Planck's constant. |
{| border="1" style="text-align: center;" | {| border="1" style="text-align: center;" | ||
| − | |+ | + | |+ Exemple of a table |
|- | |- | ||
| − | ! | + | !Color (name) |
| − | ! | + | !Frequency (Hz) |
| − | !Potencial | + | !Stop Potencial (V) |
|- | |- | ||
| | | | ||
Revision as of 18:05, 29 September 2012
Contents
Description of the Experiment
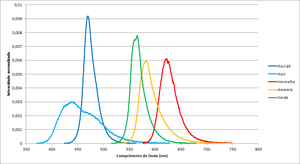
In this experiment is possible study the photoelectric effect and calculate Planck's constant. Using 5 colored leds and a photoelectric cell.
Experimental Apparatus
The photoelectric cell is from the apparatus PASCO AP-9368. It works like a capacitor where an electric conductor emits photoelectrons. The potential of the photocell will increase with the emission of photoelectrons. And the stop potential will depend on the wavelength of the incident light, photoelectric effect.
The photocell is connected to ground to discharge, after each use.
The leds have different spectrum and intensities so the time to reach the stop potencial may vary.
| Color | Frequency (THz) | Wavelegth (nm) |
|---|---|---|
| Blue.ab | 638.7 | 469.70 |
| Blue | 684.6 | 438.20 |
| Red | 482.2 | 622.21 |
| Yellow | 514.4 | 583.16 |
| Green | 530.8 | 565.22 |
Protocol
The number of photoelectrons emited will increase with the intensity of light. (corpuscular behavior of light)
- Choose a led to light up on the photocell
- Measure the stopping potential. Take note the time necessary to reach the maximum potential.
- Repit step 2 for diferent intensities.
| Color #1 __________(name) | Intensity (%) | Stop Potential (V) | Time (s) |
|---|---|---|---|
| 100 | |||
| 80 | |||
| 60 | |||
| 40 | |||
| 20 |
The photoelectron's kinetic energy depend only on the frequency of light. If the frequency of light increase the energy will increase.
- Obtain the stop potentials for different color leds.
- Make a graphic of Stop Potential vs Frequency and obtain Planck's constant.
| Color (name) | Frequency (Hz) | Stop Potencial (V) |
|---|---|---|
Protocolo Avançado
- Calcule a constante de tempo da montagem.
- Encontre os valores esperados do comprimento de onda apartir dos espectros dos leds.
- Refaça o gráfico tensão vs frequência com barras de erro.
Nota: Utilizou-se um ADC 12bit no intervalo de 0V a 5V.
Princípios Teóricos
Efeito Fotoeléctrico
O efeito foto-eléctrico consiste na emissão de electrões da superfície de um metal quando este é iluminado por luz de uma dada frequência (\( \nu \)). Um fotão de energia \( E = h \nu \) ao incidir no metal transfere a sua energia a um electrão pertencente a um dos átomos na rede cristalina do metal. A emissão de electrões do metal é muito dependente da frequência da luz incidente. Para cada metal, existe uma frequência critica, \( \nu _0 \), tal que para luz incidente com frequência inferior não há foto-electrões arrancados. Por outro lado, para frequências superiores, a energia dos foto-electrões emitidos aumenta linearmente com a energia dos fotões incidentes. A intensidade da luz incidente afecta somente o número de foto-electrões emitidos, mas não a sua energia, contrariamente ao que seria de esperar na teoria clássica da radiação. Einstein propôs a seguinte explicação para o fenómeno: a luz é transportada por fotões com uma dada energia E associada à frequência da luz \( \nu \):
\[ E = h \times \nu \]
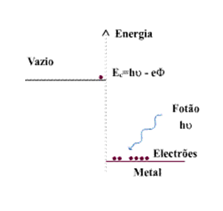
em que h é a constante de Planck. O efeito foto-eléctrico deve-se a uma colisão do fotão com o electrão, em que aquele transmite a este toda a sua energia. Tendo em conta que a energia de um electrão no vazio e dentro do metal é diferente (mais elevada no vazio), só se verifica efeito foto-eléctrico se a energia transmitida pelo fotão for superior à diferença entre estas duas energias (ver Fig. 1). Assim, a energia com que o electrão abandona o metal é igual à energia do fotão menos a energia "gasta" para o electrão abandonar o metal:
\[ E = h \times \nu - e \times \phi, \]
em que e é a carga do electrão e \( \phi \) é a diferença de workfunction. Tal como foi anteriormente enunciado, à medida que a frequência da luz incidente decresce, os fotões têm menos energia, e a partir de uma frequência critica \( \nu _0 \) não são emitidos mais foto-electrões. Neste caso, \( E _{max} = 0 \) e da Eq. l tiramos
\[ h \nu _0 = e \phi \quad ou \quad \nu _0 = \frac{e}{h} \phi \]
Efeito Fotoeléctrico
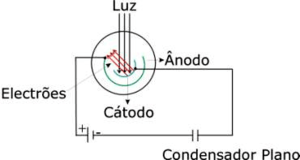
Uma célula foto-eléctrica é um dispositivo onde a luz incidente sobre uma superfície metálica (cátodo) excita electrões que vão ser colectados numa superfície metálica concêntrica (ânodo), tal como exemplificado na figura, e que na prática é um condensador semi-cilíndrico de capacidade muito baixa. Ligando o ânodo e o cátodo por um circuito externo, podemos medir a corrente produzida pelos foto-electrões. No caso mais genérico, a energia cinética máxima dos foto-electrões emitidos é determinada aplicando um potencial de paragem, Vc entre o ânodo e o cátodo de modo a impedir que os foto-electrões emitidos pelo cátodo atinjam o ânodo. Deste modo, deixa de fluir corrente no circuito.
A célula inicialmente tem aplicada a tensão da fonte, aproximadamente 9V uma vez que o condensador é descarregado no início da experiência (é efectuado um curto-circuito aos seus terminais). Como a célula está em série com o condensador, este vai carregando à medida que são gerados foto-electrões, criando uma corrente eléctrica no circuito que atravessa a célula. À medida que o condensador carrega, aumenta a diferença de potencial aos seus terminais, o que obriga a diminuir a tensão aos terminais da célula (note que \( V_{bat} = V_{Cond} + V_{célula} = constante \)). Quando a diferença de potencial nas placas da célula for igual a \( V_c = \frac{h \times \nu - e \times \phi}{e} \), deixa de fluir corrente no circuito e o condensador passa a ter uma tensão constante aos seus terminais.
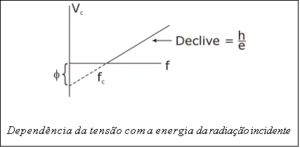
Conhecendo dois ou mais valores dessa tensão para determinadas frequências [1] pode-se efectuar uma regressão linear e determinar não só \( \phi \) mas também a constante de Planck. No gráfico seguinte esquematizamos a dependência da tensão de paragem V em função da frequência da luz incidente para um dado metal. A função em causa corresponde a uma recta de declive \( \frac{h}{e} \) e coeficiente na origem \( \phi \).
Elementos Históricos
Em 1921 foi atribuído a Albert Einstein o Prémio Nobel da Física pelas suas descobertas no efeito fotoeléctrico.