Pêndulo Mundial
Contents
Descrição
Os foguetões são enviados para o espaço a partir de latitudes equatoriais. Isto deve-se ao facto do peso aparente ser gradualmente reduzido desde os pólos até o equador. Efectivamente sentir-nos-emos mais leves no equador do que nos pólos!
É esta ligeira diferença que permite poupar toneladas de combustível quando um foguetão é lançado em órbita a partir do equador. Por exemplo, o lançamento para uma orbita geoestacionária pela Soyuz a partir da Guiana Francesa (5ºN) permite colocar 3 toneladas(ton) em órbita ao invés das habituais 1,7 ton quando lançada de Baikonur no Cazaquistão (46ºN).
O objetivo desta experiência consiste em determinar em vários pontos do globo a “constante da gravidade” através duma constelação de pêndulos colocados em várias latitudes e operados remotamente por qualquer pessoa através da internet. Espera-se que vários países da CPLP possam contribuir para esse esforço, aproximando estudantes, professores e cidadãos interessados no conhecimento físico do nosso planeta. Existem duas atividades a decorrer em paralelo: (i) o acesso através do e-lab a pêndulos em várias latitudes e (ii) a construção e operação local em escolas com o apoio da comunidade do FQ em Rede.
Lisboa, Ilhéus, Faro e Rio de Janeiro foram as primeiras cidades a contribuir para a rede em Janeiro de 2013, permitindo efectuar um ajuste dos dados experimentais à equação teórica que descreve a variação da gravidade com a latitude.
Se quiser fazer parte da rede do Pêndulo Mundial, por favor envie-nos um mail.
Ligações
- Video Faro: rtsp://elabmc.ist.utl.pt/worldpendulum_ccvalg.sdp
- Video Lisboa: rtsp://elabmc.ist.utl.pt/worldpendulum_planetarium.sdp
- Video Ilhéus: rtsp://elabmc.ist.utl.pt/worldpendulum_ilheus.sdp
- Video Rio Janeiro: rtsp://elabmc.ist.utl.pt/worldpendulum_puc.sdp
- Video Maputo: rtsp://elabmc.ist.utl.pt/wp_epm.sdp
- Video São Tomé: rtsp://elabmc.ist.utl.pt/wp_saotome.sdp
- Laboratório: Básico em e-lab.ist.eu
- Sala de controlo: Pêndulo Mundial
- Nível: *
Quem gosta desta iniciativa
Aparato experimental
Os pêndulos utilizados nas experiências são baseados no desenho do Dr. Jodl [1]. Algumas alterações menores foram introduzidas ao nível do manuseamento da massa e na adaptação a materiais simples de encontrar de forma a permitir a replicação em escolas secundárias (ensino médio). Os dados seguintes foram utilizados na sua construção:
| Caracteristícas físicas particulares | |||||
|---|---|---|---|---|---|
| Local | Latitude | Longitude | Altitude (m) | Comprimento do fio (mm) | Diâmetro da esfera (mm) |
| CCV_Algarve/Faro | 37º00'N | 7º56'W | 10 | 2677 +/- 0.5 @23ºC | 80.5 +/- 1.0 |
| UESC/Ilhéus | 14º47'S | 39º10'W | 220 | 2832.0 +/- 0.5 @23ºC | 81.0 +/- 1.0 |
| Lisbon | 38º41'N | 9º12'W | 20 | 2677 +/- 0.5 @19ºC | 80.5 +/- 1.0 |
| Maputo | 25º56'S | 32º36'E | 80 | 2609.8 +/- 0.5 @27ºC | 80.5 +/- 1.0 |
| São Tomé | 0º21'N | 6º43'E | 50 | 2756.5 +/- 0.5 @29ºC | 81.8 +/- 0.5 |
| Prague - CTU | 50º5.5'N | 14º25.0'E | 150 | 2803 +/- 0.5 @25ºC | 80.1 +/- 0.5 |
| Barcelona - UPC | 41º24.6'N | 2º13.1'E | 55 | 2824 +/- 1 | 81.8 +/- 0.1 |
| Rio de Janeiro - PUC | 22º54.1'S | 43º12'W | 50 | 2826,0 +/- 0.5 | 81.6 +/- 0.1 |
| Praia - UniCV | 14°56'N | 23°31'W | 40 | 2832,0 +/- 0.5 | 81.6 +/- 0.1 |
| Bogotá - UniAndes | 4°36'N | 74°3'W | 2500 | 2824 +/- 0.5 | 82.0 +/- 0.1 |
| Bogotá - UNAD | 4°35'N | 74°5'W | 2650 | 2835 +/- 0.5 | 82.0 +/- 0.1 |
| Panama city - UTP | 9°1.3'N | 79°31.9'W | 82 | 2825 + /- 0.5 @28ºC | 81.9 +/- 0.1 |
| Santiago - UChile | 33°27.5'S | 70°39.8'W | 552 | 2825 +/- 0.5 @27ºC | 81.9 +/- 0.1 |
| Valparaiso - UTFSM | 33°1'S | 71°37'W | 30 | 2827.5 +/- 0.5 @28ºC | 81.8 +/- 0.1 |
| Panama city - USMA | 9°1'N | 79°37'W | 130 | 2800.0 +/- 0.5 @35ºC | 81.8 +/- 0.1 |
| Brasilia - UnB | 15° 46'S | 47° 52'W | 1034 | 2826.8 +/- 0.5 @26ºC | 81.4 +/- 0.1 |
| Marseille - ECM | 43°20.6'N | 5°26.2'E | 162 | 2828.0 +/- 0.5 @22ºC | 82.0 +/- 0.1 |
| Punta Arenas - UMag | 53°8'S | 70°52'W | 40 | 2823 +/- 0.5 @16.4ºC | 81.7 +/- 0.1 |
| Características nominais | |
|---|---|
| Comprimento do cabo (raio da esfera não incluído!) | 2705mm +/- 0.5mm |
| Massa da esfera | 2kg +/- 75g |
| Diâmetro da esfera | 81.2mm +/-1.5mm |
| Cabo | Remanium(r) - Stainless steel (Nickel chromium)
- 0,4mm |
| Módulo de elasticidade do cabo | ~200GPa |
| Cronómetro | Microcontrolador com cristal de 7,3728MHz - 30ppm + laser + PIN foto-díodo |
| Wire CTE (25-500ºC) (Coeficiente expansão térmico do cabo) | ~14 x 10-6 K-1 |
A montagem experimental pode ser facilmente adaptada à operação humana para execução local, realizada apenas com o auxilio de um bom cronómetro. As estruturas de aço inox podem ser realizadas em latão ou bronze facilitando a sua talha.
O cabo empregue pode ser substituído por cabo de aço de pesca desportiva e a massa adquirida numa loja de desporto, tendo sido empregue neste caso uma de 2kg do treino do lançamento do peso olímpico. Deve ser utilizado uma fita-métrica calibrada para medir o comprimento do cabo depois de utilizar o sistema por alguns dias.
Parceiros locais
O pêndulo [2] é um dos dispositivos experimentais com maior riqueza física apesar da sua simplicidade. Efetivamente só a medida do seu cabo e a sua qualidade e dos apoios são relevantes para a construção precisa do instrumento.
Seleccionando uma massa entre 1 a 4 kg, o erro relativo ao período será suficientemente pequeno para se detetar as variações requeridas na aceleração da gravidade (inferiores a 0,1%) desde que se use um cronómetro preciso.
Uma montagem local pode ser realizada facilmente com recursos a materiais simples de encontrar e comparado o valor determinado para o "g" local com os da constelação remota de pêndulos.
A colecção destes dados através duma rede social permitirá fazer uma descrição mais precisa da variabilidade de g's em torno do globo. O "pendulo mundial" poderá ser uma importante rede colaborativa para a disseminação e o envolvimento da física nas escolas.
A construção e desenvolvimento do pendulo está detalhada em Precision Pendulum enquanto que as instruções para a sua montagem estão em Precision Pendulum Assembly.
Se quiser fazer parte da rede do Pêndulo Mundial, por favor envie-nos um mail.
Física
A determinação da aceleração da gravidade em diferentes partes do globo levanta questões sobre a importância da modelização em física. Partindo do principio que a força da aceleração é constante ao nível do mar, pode-se mostrar contudo que que esta "constante" varia ligeiramente com a latitude e tem por isso de ser corrigida consoante o lugar onde nos encontramos. Este processo permite desmistificar a ciência e corrigir o "mito urbano" existente em torno de muitas constantes que só o são com muitas aproximações. Neste caso particular mostraremos como a introdução de correcções sucessivas à "constante da gravidade" levará a valores mais próximos dos estimados experimentalmente.
Modelo geofísico
O ponto de partida é a aproximação do modelo geofísico da Terra, como sendo (i) uma esfera (ii) não-rotante cuja aproximação mais conhecida atribui o valor de 9,81 ms-2. É trivial notar que este modelo, devido à simetria da esfera, leva a valores uniformes em qualquer latitude da Terra. Mas assim que introduzimos a dinâmica do movimento terrestre aperceber-nos-emos que este valor passa a depender da latitude bem como se considerarmos a terra um elipsóide devido ao achatamento nos pólos. Com efeito estes dois aspetos são as principais causas do desvio da "constante da gravidade" com a latitude [1] e superam todos os outros efeitos tais como (i) a altitude do lugar, (ii) as marés ou (iii) a constituição do sub-solo próximo ao lugar.
Para demonstrar estes aspetos mais finos, a aceleração da gravidade tem de ser determinada em várias latitudes sobre o globo e bastante afastadas entre si. Com estas medidas obtidas em rede, os alunos poderão questionar-se sobre a "constante" e interpretar melhor a força da gravidade.
Estudos experimentais
Variação com a latitude
Como se viu, o primeiro estudo possivel consiste na utilização dos pêndulos remotos e verificar qual a aceleração da gravidade aparente nesses vários locais. Através da introdução (ou desprezo) de vários ajustes tenta-se chegar graficamente a um ajuste da descrição experimental da terra usando harmónicos esféricos (equação \eqref{harmonica-esferica}). Este estudo pode ser conduzido usando a constelação de pêndulos do e-lab e de outros parceiros.
Determinação local
Seguindo as instruções descritas nesta wiki - Precision_Pendulum - ou usando outro tipo de construção rigorosa dum pêndulo, produz-se e instala-se um pêndulo local e contribui-se para o enriquecimento da folha de cálculo da rede do pêndulo mundial.
Estudo das marés
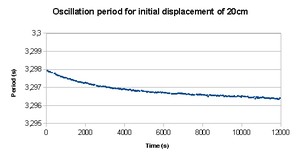
Com base num almanaque [3] obtém-se as datas/horas dos dias de alinhamento da lua com o Sol (marés vivas ou lua-cheia e lua nova) e quando estamos em quarto crescente ou minguante. Traçando um gráfico ao longo de vários meses tenta-se verificar e quantificar a influência das marés e do alinhamento da Lua com o Sol no peso aparente. Desta forma pode-se tentar associar às marés (luas) e ao movimento de translação eventuais flutuações medidas na aceleração aparente da gravidade, fazendo um estudo com um período mensal e/ou anual (p.exemplo ver as diferenças no periélio de Janeiro c/ lua nova e no afélio de Julho com lua cheia). O efeito de maré está no limite da deteção dos pendulos usados pelo que é necessário um grande rigôr na hora (a influência solar é muito superior à lunar mas a flutuação é inferior) e o emprego de técnicas numéricas avançadas usando por exemplo a transformada de Fourier.
Análise da torção no fio
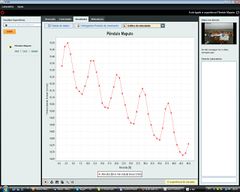
Para os mais atentos, a velocidade na origem apresenta uma variação devido à torção do fio e à não-esfericidade da massa. O gráfico anexo demonstra isso. Pode ser efetuado o estudo do pêndulo considerando a massa da bola e a torção no fio, recomendando-se o uso das equações de euler-lagrange.
Movimento circular uniformemente acelerado
A velocidade de transito da esfera no ponto inferior da trajetória é determinada pela medida do tempo de interrupção do feixe laser. Com efeito, sabendo o diâmetro da esfera é imediato determinar a velocidade na origem podendo ser inferida a energia cinética máxima. Deste modo, sabendo o comprimento do cabo, pode-se calcular o ponto de lançamento da esfera e confrontar com o ponto de lançamento.
Provedores de latitude"
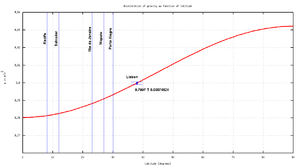
A língua é um fator importante da nacionalidade ("a minha pátria á a língua portuguesa", F. Pessoa) e uma maneira simples de definir os chamados "países irmãos". Na prática só quatro línguas estão disseminadas no globo, sendo uma delas o português. Naquilo que nos interessa, o português cobre latitudes de ~30ºS a ~42ºN, quase 75º de variação sobre o equador. Deste modo os países da CPLP poderão servir como "provedores de latitude" (ver figura).
Para realizar esta experiência e ajustar pontos relevantes à nossa curva experimental precisaremos de pelo menos quatro pontos espaçados em latitude. Mas devido à não-linearidade da equação mais pontos serão convenientes para obter um ajuste firme, principalmente em torno do "joelho" nas latitudes de 10º-30º. Só o Brasil por si permite obter grade parte deste conjunto de pontos (Recife 8º, Salvador – 12º, Rio de Janeiro – 23º, Porto Alegre – 30º) mas não permite suprir os pontos onde a aceleração da gravidade varia mais rapidamente, a região quase linear entre 30º e 60º onde Portugal pode contribuir com dois pontos, por exemplo 37º e 41º. Moçambique e Angola podem contribuir com pontos redundantes próximos ao equador e S. Tomé e Príncipe, Brasil e Cabo Verde com valores equatoriais.
Ajuste experimental
Existem inúmeras fontes de informação sobre o pêndulo [2] [4] [5] [6] [7] [8]. Se forem tidas em conta todas as influências significativas a equação harmónica na latitude que resulta pode ser expressa por:
[math] g_{n}(\varphi) = 9.780 326 772\times[1 + 0.005 302 33 \cdot sin^{2}(\varphi) - 0.000 005 89 \cdot sin^{2}(2\varphi)] \label{harmonica-esferica} [/math]
onde \(\varphi\) é a latitude do lugar. Esta expressão é uma das que melhor ajusta os resultados experimentais de acordo com o "World Geodetic System datum surface (WSG84)", considerando a terra como um elipsóide de raio r1=6378137m no equador e r2=6356752m como o raio semi-menor polar.
Propõe-se que se derive pelo menos a correção devido à força centrífuga e do achatamento dos pólos.
Na figura mostra-se o desvio da "constante da gravidade", ou seja o valor real em função da latitude. Estão marcadas as latitudes de alguns possíveis parceiros. Houve a preocupação de evitar que qualquer erro experimental excedesse os 0,05%, tendo em conta um desenho preciso da montagem experimental de forma a conseguir obter a precisão final mínima de 0,1% para poder comparar os dados.
Notas históricas
A importância do pêndulo como elemento base dos relógios e cronografos só foi destronada quando a Royal Society convenceu o parlamento inglesa a instituir um prémio de 10k£ a 20k£ (atualmente mais de 3,5M€) para a invenção dum cronografo que não dependesse dele. Com efeito a precisão do pêndulo na determinação do tempo só é ultrapassada por sistemas eletrónicos modernos.
Efetivamente, à data dos descobrimentos, a longitude só era determinada com um elevado erro, uma vez que os relógios e cronografos dependiam do pendulo e este era muito sensivel às oscilações dos navios, alterando a sua frequência ou até parando. A hora local do navio era utilizada para comparar com a hora solar (ou estelar) e com esta diferença estabelecia-se a longitude do lugar.
Bibliografia
- ↑ 1.0 1.1 World pendulum—a distributed remotely controlled laboratory (RCL) to measure the Earth's gravitational acceleration depending on geographical latitude, Grober S, Vetter M, Eckert B and Jodl H J, European Journal of Physics - EUR J PHYS , vol. 28, no. 3, pp. 603-613, 2007
- ↑ 2.0 2.1 Physics for scientists and engineers, 5th edition, Hardcourt College Publishers, R.Serway and R. Beichner, 2000
- ↑ http://www.oal.ul.pt/index.php?link=dados2012
- ↑ http://rcl-munich.informatik.unibw-muenchen.de/
- ↑ Nelson, Robert; M. G. Olsson (February 1987). "The pendulum - Rich physics from a simple system". American Journal of Physics 54 (2): doi:10.1119/1.14703
- ↑ Pendulums in the Physics Education Literature: A Bibliography, Gauld, Colin 2004 Science & Education, issue 7, volume 13, 811-832 (http://dx.doi.org/10.1007/s11191-004-9508-7)
- ↑ The exact equation of motion of a simple pendulum of arbitrary amplitude: a hypergeometric approach, M I Qureshi et al 2010 Eur. J. Phys. 31 1485(http://dx.doi.org/10.1088/0143-0807/31/6/014)
- ↑ A comprehensive analytical solution of the nonlinear pendulum, Karlheinz Ochs 2011 Eur. J. Phys. 32 479 (http://dx.doi.org/10.1088/0143-0807/32/2/019)