Langmuir Probe
Contents
Description of the Experiment
Plasmas have different characteristics from other states of matter and in order to measure their parameters many diagnostic tools have been developed. This experiment allows the measurement of some of these characteristics using one of the most simple methods, an electrical probe, the Langmuir probe. It consists of a thin filament made of conductive material placed inside the plasma which either attracts or repels the electrons in the plasma according to its polarization. Measuring the probe I-V characteristic, that is the relationship between the polarization voltage and the respective collected current, one can determine the electron temperature and density of the plasma.
|
Ligações
|
Videos The #evp parser function was deprecated in EmbedVideo 2.0. Please convert your parser function tag to #ev.
|
Experimental Apparatus
The vacuum chamber consists of a Pyrex cylinder on which a glow discharge is produced by RF power. A tungsten filament with 0.2mm in diameter is placed in the middle of the chamber partially isolated by an alumina cover and only a 10mm tip is exposed to the plasma acting as a Langmuir probe. This central filament as a ground reference around the probe with approximate 200mm in order to be much longer than the probe itself.
The RF generator (3.5W, 50kHz, 1kV) which ionizes the gas and generates the plasma is connected to two parallel molybdenum plates similar to a capacitor.
Protocol
Determination of the electron temperature and density
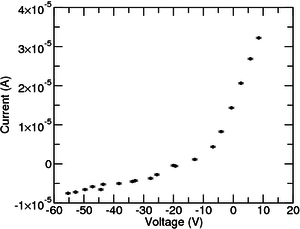
The Langmuir probe uses one or more electrodes placed inside the plasma to measure the current collected while applying a voltage. This will provide the I-V characteristic for that plasma. Normally a triangular or sawtooth wave is used to get equi-separated points.
When the probe is electrically isolated, a plasma sheath is formed in the interface between the plasma and the probe. To compensate for the higher mobility of the electrons the probe will attain a floating potential,\(V_f\), negative with respect to the plasma potential itself, \(V_p\). The density at the sheath entrance is roughly half of the density away from the probe.
The probe voltage, \(V_s\), is sweeped with respect to the ground winding filament using a variable voltage source. If the polarization of the probe compared to the plasma potential is negative enough all the electrons will be repelled and the ion flux to the probe is independent of the potential applied. In a totally ionized plasma this ion saturation current is described by the following expression: \[ i^+_{sat} = j^+_{sat} A_s = \frac{e \, n \, c_s \, A_s}{2} \]
Where \(j^+_{sat}\) is the ion current density, \(A_s\) is the contact surface of the probe, \(e\) is the electron charge, \(n\) is the ion density in the plasma, \(c_s\) is the ion sound speed.
When the polarization applied to the probe is increased, the voltage drop in the sheath is reduced and electrons will be able to reach the probe. Taking a Maxwell distribution for the speed of the electrons, the relation between current and tension will be: \[ i = -i^+_{sat} \left( 1- e^{\dfrac{e}{k T_e} (V_s - V_f)} \right) \]
Where \(T_e\) is the electron temperature. This expression assumes that there is only one probe and that it is non-perturbative.
From the last equation it is possible to extract an estimate for the floating potential, \(V_f\). This is done by taking the value at which the characteristic crosses zero.
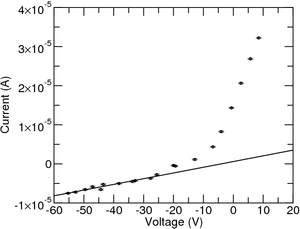
It will also be easily seen that the data does not follow the regular characteristic on the ion saturation side, it should be constant instead of having a slope. This has to do with the fact that the sheath thickness expands with the applied voltage. To correct for this, a linear function is fitted on this side and the slope is subtracted (as seen in Figure 3). Alternatively we can include this contribution in the equation:
\[ i = -i^+_{sat} \left( 1- \alpha\ (V-V_f) - e^{\dfrac{e}{k T_e} (V_s - V_f)} \right) \]
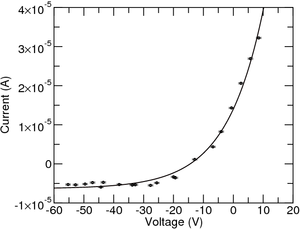
However, we want to get the density, so we have to make another correction, which corresponds to add the value of current in point where we know the current is completely due to ions, namely to voltage values much lower than the floating potential (in this case we use two times the floating potential, hence the need for our initial estimate).
After that, the experimental data has to be adjusted to the equation presented in above (as seen in Figure 4). From the fit the \(T_e\) can be extracted as well as the ion saturation current, \(i^+_{sat}\) and the floating potential \(V_f\) which should have a value close to the one we determined empirically.
By knowing the area of the probe and the speed of sound in the ions of the plasma, one can determine the electron density in the plasma. Since \(c_s = \sqrt{\dfrac{k T_e}{M}}\), and the fact that the probe is \(10mm\) and has a diameter of \(0.2mm\) we can use the \(i^+_{sat}\) to determine the density.
Links
Principles of Plasma Diagnostics, Hutchinson, Cambridge