Free Fall (determination of the standard gravity)
Contents
Description of the Experiment
This experiment allows you to determine the standard gravity acceleration, g .
Links
- Video: rtsp://elabmc.ist.utl.pt:554/g.sdp
- Laboratory: Basic in e-lab.ist.eu
- Control room: g
- Grade: ***
<swf height="270" width="480">http://www.elab.tecnico.ulisboa.pt/anexos/descricoes-flash/Gravidade.swf</swf>
Experimental Apparatus
This apparatus consists in a projectile launcher (with an electromagnet) that vertically ejects a ping-pong ball from the base.
The ping-pong ball is launched from the base with a certain kinetic energy selected by the user (energy applied to the electromagnet) and executes the typical parabola trajectory, falling subsequently on the base. The height (vertical coordinate) is measured and recorded with an ultrasound sonar, strategically placed above the experiment, measuring the distance to the ball. With the resulting data it is possible to determine g. The ball is sometimes launched with a small horizontal component, but this does not affect measurements (why?).
Since the height is measured by ultrasounds, the actual time between samples varies from the one provided by the user: the closer the ball is to the sensor (i.e., higher), the shorter the time between samples is. This can be negleted unless a precise fitting is required.
Protocol
The user must define the following parameters: launch energy, time between samples and number of samples.
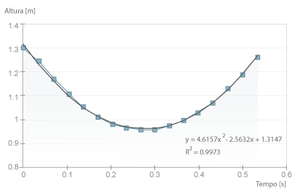
The standard gravity, g, can be established in several ways. The simplest one is to fit the mathematical law for the ball's motion, \( x = x_0 + v_0 t + \frac{1}{2}gt^2 \), to the experimental data by choosing three points from the space-time graph and solving the system of equations.
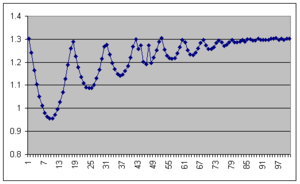
The following graph is a raw data example with \( 20 ms \) between samples.
The next graph is a fitting over one trajectory, with the corrected time and numerical fitted curve, giving the final value of \( 9,2\pm 0.8 ms^{-2} \) for g.
Advanced Protocol I
Since the ping-pong ball has a very low mass, the air resistance will be significant after the ball reaches a certain speed. This way, if we fit the \( x = v_0 t + \frac{1}{2} g t^2 \) to the data right as the motion starts (\(v_0 \simeq 0\)), we can obtain a numerical value for g that is closer to reality. It is interesting to study on how g changes with speed and observe its deviation from the expected value \( 9.8 m/s^{-2} \). It can be observed that for smaller trajectories (when the ball bounces), the numerical results are better, or, likewise, in regions where the speed is lower (when the ball reaches a maximum in height).
Considering air friction, the fitting of a more adequate function will result in a more precise value for \( g \) and will allow the determination of the air friction constant alpha (\( \alpha \)). The force of friction is dependant of \( v^2 \) and is always opposite to the movement. Balancing this force and the force of gravity we can consider the differential equation:
[math] mg - \alpha v^2 = ma [/math] .
Advanced Protocol II
The restitution coefficient can be inferred from consecutive leaps. It can be used to determine the energy loss in every ball collision and to study its behavior.