Queda de Graves (determinação de g)
Contents
Descrição da Experiência
Este laboratório permite determinar a constante de aceleração da gravidade, g.
<swf height="270" width="480">http://www.elab.tecnico.ulisboa.pt/anexos/descricoes-flash/Gravidade.swf</swf>
Ligações
- Video: rtsp://elabmc.ist.utl.pt:554/g.sdp
- Laboratório: Básico em e-lab.ist.eu
- Sala de controlo: g
- Nivel: ***
Aparato experimental
A montagem consiste num lançador de projéctil, baseado num electroíman que lança uma bola de pingue-pongue na vertical a partir de uma base.
A bola efectua a sua trajectória e acaba por cair na base de novo. A determinação da altura da bola é efectuada por um sonar de ultra-sons, colocado por cima da experiência, que mede a distância entre si e a bola. Com a aquisição da coordenada vertical do projéctil é possível determinar a constante da aceleração gravitacional.
A bola de pingue-pongue é lançada com uma energia inicial escolhida pelo utilizador (a energia aplicada ao electroíman) e, com um registador ultra-sónico de posição, é determinada a sua coordenada vertical em função do tempo. Note-se que a bola por vezes parte com uma pequena componente horizontal, mas tal não afecta as medidas. Uma vez que a altura da bola é determinada por um efeito de radar ultra-sónico, o tempo entre amostras varia pelo que é disponibilizado ao utilizador, que poderá facilmente verificar que diminui com a proximidade da bola ao sensor (maior altura).
Protocolo
Os parâmetros a definir são a energia de lançamento, o tempo entre amostras e o número de amostras a tirar.
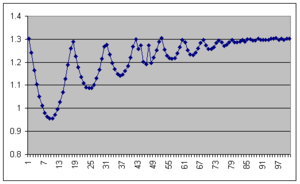
A aceleração da gravidade, g, pode ser estabelecida de várias maneiras. A mais simples é estabelecer a lei do movimento para a bola de pingue-pongue, \( x = x_0 + v_0 t + \frac{1}{2}gt^2 \), e com base no gráfico espaço-tempo, extrair três pontos e resolver o sistema obtido. A figura seguinte é um exemplo dos dados em bruto obtidos com \( 20 ms \) entre amostras:
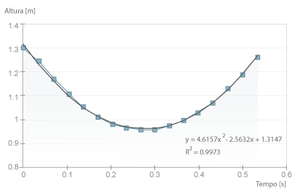
No próximo gráfico, onde já consta o tempo corrigido, é feito o ajuste numérico com a opção linha de tendência do Excel, sendo obtido o valor \( 9,2 ms^{-2} \).
Protocolo Avançado
Uma vez que a bola de pingue-pongue é muito leve, a acção da resistência do ar (atrito) far-se-á sentir logo que a bola adquira uma certa velocidade. Deste modo, se se ajustar a função \( x = v_0 t + \frac{1}{2} g t^2 \) a partir do início da queda (v_0 \simeq 0), obter-se-á um valor para g mais próximo da realidade. É interessante fazer um estudo da variação de g com a velocidade e observar o seu desvio em relação ao valor esperado de \( 9,8 m/s^{-2} \). Observe que para trajectórias menores (ressaltos da bola) o ajuste na generalidade melhora, ou, equivalentemente, para uma região em torno de velocidades baixas (quando a bola passa por um máximo de altura). Ao considerar o atrito, o ajuste da função adequada permitirá extrair não só o valor de g com a máxima precisão, mas também determinar a constante alfa ( \( \alpha \) ) de atrito. Suponha-se que o atrito depende de \( v^2 \) e actua como uma força de retardamento, de acordo com a equação diferencial: \( mg - \alpha v^2 = ma \).