Estatística de Dados
Contents
Descrição
Esta experiência consiste num sistema automático de lançamento de dados de seis faces. Para se contarem as pintas, procede-se à aquisição e análise automática da imagem destes dados.
Os valores permitem estudar a lei das probabilidades e elaborar um estudo estatístico de fenómenos aleatórios. Pode-se, também, utilizar as imagens para desenvolver algoritmos próprios, aplicando os mesmos no estudo de várias ferramentas de visão por computador.
Ligações
- Video: [indisponível]
- Laboratório: Básico em e-lab.ist.eu[1]
- Sala de controlo: Aleatório
- Nivel: ***
<swf height="320" width="320">http://www.elab.tecnico.ulisboa.pt/anexos/descricoes-flash/EstatisticaDados.swf</swf>
Aparato Experimental
A experiência consiste num altifalante posicionado na horizontal com uma plataforma no topo do cone de k-line (cartão estruturado com poliuretano), onde se encontram espalhados 14 dados. Na parte superior, a 30 cm da plataforma, está uma câmara de vídeo e um led branco de alto brilho para iluminar a plataforma.
O lançamento dos dados é conseguido através da excitação do altifalante com uma onda sonora, vibrando a plataforma com a mesma frequência da onda.
Esta plataforma tem uma parede que impede os dados de saírem da plataforma e do campo de visão da webcam. Esta parede é bastante alta, para impedir a entrada de luz que não provenha do seu sistema de iluminação.
Com este aparato, obtêm-se imagens como a da figura 2.
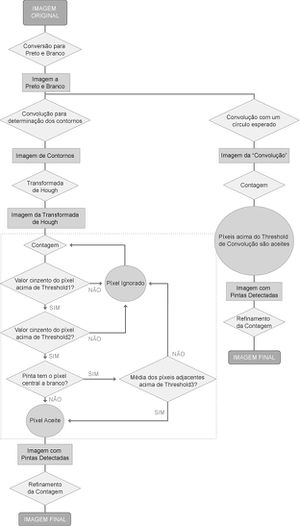
O processamento desta imagem é feito segundo o fluxograma abaixo e o resultado deste processamento leva a uma imagem como a da figura 3.
Protocolo
O protocolo de execução da experiência é simples porque consiste em excitar, convenientemente, a plataforma para que esta consiga baralhar os dados. De seguida, descreve-se os principais elementos do configurador da sala de controlo para uma melhor compreensão dos mesmos.
Manual de Utilização
É possível escolhermos os parâmetros todos da análise de imagem.
- Black&White Threshold: para definir o valor, em escala de cinzento, acima do qual os pixéis ficam a branco.
- Para a Transformada de Hough:
- Threshold1: define o valor acima do qual um pixel da imagem da transformada de Hough é considerado para análise posterior;
- Threshold2: faz a média dos pixéis na vizinhança do pixel que passou o teste anterior e, se essa média for acima deste Threshold2, esse pixel é considerado para análise posterior;
- Threshold3: à partida, qualquer pixel detectado numa zona a branco do dado é desprezado, mas, se esse pixel apresentar uma média (calculada para o teste anterior) superior a este Threshold3, então esse pixel é aproveitado. Isto, porque os dados têm, por vezes, o centro das pintas a branco.
- Convolution Thresold: define o valor acima do qual um pixel da imagem da convolução é considerado para análise posterior;
- Propriedades dos dados:
- Raio da pinta: raio esperado, em pixéis, para a(s) pinta(s) do(s) dado(s) (Nota: Este algoritmo espera que as pintas sejam circulares).
- Largura do dado: distância máxima, em pixéis, entre pintas. Ou seja, para dados de 6 pintas, esta será a distância duma pinta num canto ao outro, na diagonal.
- Número de dados esperado: quantidade de dados esperada. Se for detectada uma quantidade superior e alguns desses não forem detectados como "compatíveis" com dados, então estes serão eliminados (Nota: O algoritmo compara as posições das pintas com conjuntos detectados, com base na proximidade das pintas. Estes conjuntos são comparados com o que se espera obter num dado com a quantidade de pintas que esse conjunto tiver; se essa comparação der positiva, o conjunto fica marcado como "compatível", se não tenta-se fazer trocas e/ou eliminação de pintas até se obter conjuntos "compatíveis" com dados).
Som (lançamento dos dados)
Os dados são lançados (baralhados) pelo movimento oscilante da plataforma onde se encontram. Pode-se seleccionar as frequências inicial e final da onda sonora que vai ser transmitida à plataforma de lançamento dos dados. Esta onda é gerada na altura, ou seja, não há uma colecção de ficheiros de som que já estão gravados com todas as combinações possíveis.
A frequência mínima possível é 20 Hz e a máxima é de 150 Hz.
Abaixo de 20 Hz, não há resposta do altifalante, do amplificador, nem da placa de som que permita a vibração da plataforma. Acima dos 150 Hz, por inércia, a vibração da plataforma tem uma amplitude muito reduzida, logo não é suficiente para comunicar movimento aos dados.
Escolhemos também a duração desta onda sonora, com um mínimo de 1.5 s e um máximo de 10 s. 1.5 s é suficiente para os dados se baralharem um pouco mas para certas frequências perto dos limites, são poucos os que mudam a face virada para cima. 10 s já permite que haja uma desordem dos dados bastante elevada embora desnecessária na maioria dos casos.
Imagem
Escolhemos quantas imagens pretendemos analisar, ao escolher o número de amostras. No mínimo podemos ter uma amostra e, no máximo, vinte.
Uma amostra serve para verificarmos como funciona o motor de detecção, quais os passos que ele segue e quanto tempo demora em cada passo. Com vinte amostras é possível vermos a distribuição que se espera aproximar à “gaussiana” (apesar de tal só acontecer, em teoria, para trinta amostras, pelo menos).
Video
Podemos escolher ver ou não o vídeo do processo de baralhar os dados.
Este vídeo é composto por uma sequência de imagens em formato .jpeg, logo não é um vídeo no verdadeiro sentido da palavra, podendo demorar a transferência de dados de acordo com a velocidade da rede.
Visto que o vídeo exige uma elevada utilização da largura de banda disponível, é aconselhável o seu uso apenas para uma amostra e para ver uma única vez, com intuito lúdico, dado que se torna repetitivo.
Protocolo Avançado
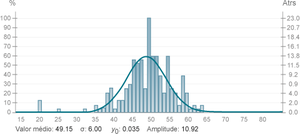
Após a aquisição de suficientes contagens, constrói-se um gráfico do número de ocorrências e faz-se um ajuste à função de distribuição Gaussiana esperada, representada por:
<math> p(x) = y_0 + A e ^{- \frac{(x- \mu)^2}{\sigma ^2}} \]
Como se têm 14 dados, espera-se que o valor mais provável seja 49, o que é comprovado por este ajuste efectuado pela acumulação de valores.
A melhor forma de realizarmos este estudo é articular os resultados de vários utilizadores e verificarmos como melhora o ajuste em função do número crescente de amostras adicionadas.
O valor esperado para o valor médio do lançamento de N dados de seis faces é dado por:
<math> \bar{\mu} = \frac{6N+N}{2} \]
Estudo da frequência ideal para excitar os dados
Suposições:
- O dado que parte do repouso acompanha o movimento ascendente da plataforma;
- O dado apenas se separa da plataforma quando esta começa a descer, ou seja, o dado fica em queda livre, com velocidade inicial vertical nula;
- O choque do dado com a plataforma é inelástico, ou seja, volta a acompanhar a plataforma até à seguinte posição máxima desta.
Assim, partindo do momento em que o dado larga a plataforma, ou seja, quando esta começa a descer, podem-se escrever as seguintes expressões para os movimentos do dado e da plataforma:
Dado: \( y(t) = \frac{A}{2} - \frac{g ^2}{2} \)
Plataforma: \( y'(t) = A cos(2 \pi f t) \)
Nestas expressões: A é a amplitude com que a plataforma vibra; g é a aceleração da gravidade; f é a frequência de vibração da plataforma e t é o tempo desde o momento indicado anteriormente.
Igualando e resolvendo em ordem a t, obtém-se a seguinte equação implítcita:
<math> t = \sqrt{\frac{A- 2 A cos (2 \pi f t)}{g}} \]
Para resolver esta equação, usou-se um método numérico que, essencialmente, tendo um valor de t inicial, avalia a raiz e atribui o valor encontrado à variável t. Volta a repetir este processo até que o valor de t convirja. Obviamente, tem que se ter os valores da amplitude, da frequência e da aceleração da gravidade fixos; usou-se, para a amplitude, 3 mm; para a frequência, usaram-se várias entre 1 e 500 Hz e para a aceleração da graviadade, usou-se 9,81 \(ms^{-2}\).
O valor de t usado para a primeira iterada é de 1/4f, para que o coseno, dentro da raiz, dê zero e a primeira iterada dê um valor real.
Na seguinte tabela estão indicadas as frequências e t para as quais o método convergiu, tal como os cos e sin correspondentes:
| f (Hz) | t (miliseg.) | cos(2p f t ) | - sin(2p f t ) |
|---|---|---|---|
| 14 | 27.91 | -0.7732 | -0.6341 |
| 15 | 29.70 | -0.9418 | -0.3362 |
| 16 | 30.24 | -0.9948 | -0.1017 |
| 17 | 30.25 | -0.9960 | 0.0893 |
| 18 | 29.98 | -0.9692 | 0.2462 |
| 19 | 29.54 | -0.9268 | 0.3756 |
| 20 | 29.01 | -0.8758 | 0.4827 |
| 21 | 28.42 | -0.8206 | 0.5715 |
| 49 | 30.21 | -0.9924 | 0.1227 |
| 50 | 30.26 | -0.9968 | 0.0805 |
| 51 | 30.06 | -0.9781 | 0.2083 |
| 83 | 30.26 | -0.9973 | 0.0736 |
| 116 | 30.27 | -0.9977 | 0.0680 |
| 149 | 30.27 | -0.9980 | 0.0632 |
| 182 | 30.27 | -0.9983 | 0.0591 |
| 215 | 30.27 | -0.9985 | 0.0554 |
| 248 | 30.28 | -0.9986 | 0.0521 |
| 281 | 30.28 | -0.9988 | 0.0491 |
De notar que, regra geral, as trajectórias cruzam-se perto do mínimo da trajectória da plataforma (cos(2pf t ) >> -1), já quando esta vai a subir (-sin(2p f t ) >0).