Conservação do Momento Angular
Contents
Descrição da Experiência
Esta sala de controlo permite verificar a conservação do momento angular e medir o momento de inércia de um conjunto de discos em rotação.
Aparato Experimental
O aparato experimental consiste num disco rígido de computador ao qual foram adicionados um servo e um conjunto de discos suspensos por este. Esta montagem permite a realização do primeiro protocolo experimental, centrado no estudo da conservação do momento angular.
O aparato conta ainda com um conjunto de resistências de travagem que podem ser colocadas em paralelo com os enrolamentos do motor do disco por um relé. Esta montagem permite a realização do segundo protocolo experimental, centrado no estudo do momento de inércia.
Protocolo
5 discos com 115g no total são acelerados pelo motor do disco rígido até 1500rpm. Neste momento o motor desliga-se, os discos ficam a rodar livremente e a sua velocidade de rotação vai sendo adquirida. Quando for atingida uma velocidade escolhida previamente pelo utilizador, o servo deixa cair sobre os discos em rotação 3 discos com 69g no total inicialmente em repouso.
No final da sessão obtém-se uma tabela com a velocidade dos discos em função do tempo, cujos valores servirão para criar um gráfico num programa ao critério do utilizador.
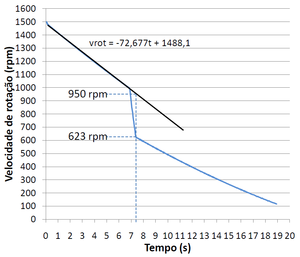
O gráfico à direita foi criado no Microsoft Excel a partir da tabela de resultados de uma experiência em que o servo deixa os discos cair a 1000 rpm. Fazendo uma regressão entre o início da desaceleração e a queda dos discos, obtém-se uma reta cuja equação nos permite determinar a velocidade prevista dos discos em rotação no ponto em que os discos que caem deixam de deslizar sobre os que estavam em rotação.
Temos para a conservação do momento angular:
\[ L_i=L_f \] \[ I_i w_i=I_f w_f \] \[ \frac{I_i}{I_f}=\frac{w_f}{w_i} \] \[ \frac{\frac{m_i\left (r_1^2+r_2^2 \right )}{2}}{\frac{m_f\left (r_1^2+r_2^2 \right )}{2}}=\frac{w_f}{w_i} \]
No exemplo da figura onde foram lançados os segundos discos a partir do instante 3 s, é efectuada uma regressão linear sobre os pontos iniciais antes de ocorrer o acoplamento dos discos. Obtida esta equação (p.ex. utilizando a função linha de tendência do Microsoft Excel) é possível extrapolar o que seria a velocidade no instante 5.5 s onde ambos os discos já rodam à mesma velocidade. Neste caso obter-se-ia uma velocidade de cerca de 3215 rpm. Consultando o valor na tabela para este instante, obstem-se uma leitura de 2010 rpm. A razão (2010/3215) deverá ser equivalente à razão das massas (3/5).
Protocolo Avançado
Esta experiência permite actuar um travão electromagnético que consiste em três resistências eléctricas que dissipam a energia gerada pelo motor a funcionar como gerador (tal como um dínamo de uma bicicleta). Este travão é actuado numa altura pré-determinada, o que origina uma forte desaceleração dos discos a partir desse instante. Comparando a desaceleração (variação da energia cinética de rotação) dos discos com a energia dissipada é possível estimar o momento de inércia I dos discos. O modo mais expedito consiste em integrar a potência dissipada, obtendo a energia dissipada ao longo do tempo; esta terá de ser igual à variação da energia cinética de rotação entre os instantes de integração considerados.
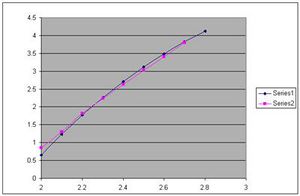
Gráfico do ajuste à serie 1 que representa a energia dissipada integrando a potência em função do tempo pela serie 2 obtida com o ajuste da função \[ E = \frac{I \omega ^2}{2} \] onde I é o parâmetro a ajustar. Com a definição do momento de inércia para um disco homogéneo presente: \[ I = \frac{m r ^2}{2} \] determina-o para a massa do raio do disco inicial e compara com o valor experimental obtido pelo balanço energético descrito no parágrafo anterior. É ainda interessante discutir qual a perda relativa de energia na colisão e se é possível afirmar que existe conservação do momento e da energia.