Sonda de Langmuir
EM CONSTRUÇÃO
Contents
Descrição da Experiência
Os plasmas têm características diferentes de outros estados da matéria pelo que muitas ferramentas de diagnóstico foram desenvolvidas a fim de as medir. Esta experiência permite determinar algumas destas características através de um dos métodos mais simples, uma sonda eléctrica, a sonda de Langmuir. Esta é constituída por um filamento fino feito de material condutor que é colocado no interior do plasma, e que atrai ou repele os electrões do plasma de acordo com a sua polarização. A partir da análise da característica eléctrica da sonda, que é a relação entre a tensão de polarização e da respectiva corrente colectada, é possível determinar a temperatura dos electrões e da densidade do plasma.
|
Links
|
Videos |
Aparato Experimental
A câmara de vácuo é composta por um cilindro de pirex na qual uma descarga de luminescência é produzida por radiofrequência. Um filamento de tungsténio com um diâmetro de 0.2 mm é colocado no meio da câmara parcialmente isolado por uma camada de alumina deixando somente uma ponta 10 mm exposta ao plasma, actuar como uma sonda de Langmuir. Este filamento central tem uma referência de terra em torno da sonda com cerca de 200mm, de modo a ser muito maior do que a própria sonda.
O gerador de radiofrequência (3.5W, 50kHz, 1 kV), que ioniza o gás e gera o plasma, é ligado a duas placas de molibdénio paralelas semelhantes às de um condensador.
Protocolo
Determinação da temperatura e densidade electrónica
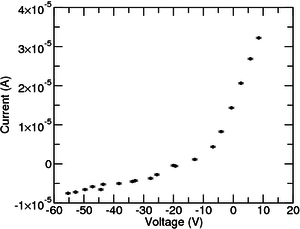
A sonda de Langmuir utiliza um ou mais eléctrodos colocados no interior do plasma para medir a corrente coletada durante a aplicação de uma tensão de polarização. Isto irá fornecer a característica IV do plasma. Normalmente, é usado um sinal triangular ou dente de serra para obter pontos equi-separados.
Quando a sonda está isolada electricamente, forma-se uma bainha electrica na região de interface entre o plasma e a sonda. Para compensar a maior mobilidade dos electrões, a sonda vai atingir um potencial flutuante, \(V_f\), negativa em relação ao potencial de plasma, \(V_p\). A densidade na entrada da bainha é de aproximadamente metade da densidade longe da sonda (critério de Bohm).
A tensão de sonda em relação ao enrolamento de referência, \(V_s\), é varrida utilizando uma fonte de tensão variável. Se a polarização da sonda, comparado com o potencial do plasma, for bastante negativa todos os electrões serão repelidos e o fluxo de iões para a sonda é independente do potencial aplicado. Num plasma totalmente ionizado, esta corrente de saturação de iões é descrita pela seguinte fórmula: [math] i^+_{sat} = j^+_{sat} A_s = \frac{e \, n \, c_s \, A_s}{2} [/math]
Em que \(j^+_{sat}\) é a densidade de corrente iónica, \(A_s\) a superfície de contato da sonda, \(e \) a carga do electrão, \(n\) a densidade iónica da plasma, e \(c_s\) a velocidade do som dos iões.
Quando a tensão de polarização aplicada à sonda aumenta, a queda de potêncial na bainha é reduzida e os electrões serão capazes de alcançar a sonda. Assumindo uma distribuição de Maxwell para a velocidade dos electrões, a relação entre corrente e tensão será: [math] i = -i^+_{sat} \left( 1- e^{\dfrac{e}{k T_e} (V_s - V_f)} \right) [/math]
Em que \(T_e\) é a temperatura electrónica. Esta expressão assume também que há apenas uma sonda e que esta é nao perturbativa.
A partir da última equação é possível extrair uma estimativa do potencial flutuante, \(V_f \). Isto é feito tomando o valor no qual a característica cruza o zero.
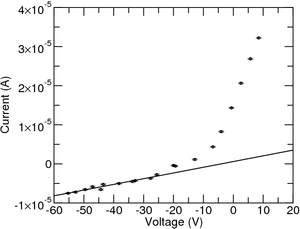
Também se verifica facilmente que os dados não acompanham a característica do lado da saturação iónica, que devia ser constante em vez de ter um declive. Isto tem que ver com o facto de que a largura da bainha aumenta com a tensão aplicada. Para corrigir isto ajusta-se uma função linear desse lado e de seguida subtrai-se o declive desta (como pode ser visto na Figura 3). Alternativamente pode-se incluir essa contribuição na equação: [math] i = -i^+_{sat} \left( 1- \alpha\ (V_s-V_f) - e^{\dfrac{e}{k T_e} (V_s - V_f)} \right) [/math]
No entanto, quer-se obter a densidade, de modo que é necessário fazer uma outra correção, corresponde à soma do valor da corrente no ponto em que você sabe que a corrente é completamente devida aos iões, ou seja, para valores de tensão muito menores do que o potencial flutuante (tipicamente usa-se duas vezes o potencial flutuante, daí a necessidade de nossa estimativa inicial).
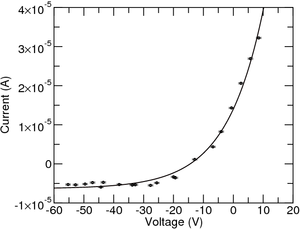
Depois disso os dados experimentais têm de ser ajustados à equação apresentada anteriormente (como se vê na Figura 4). A partir do ajuste \(T_e \) pode ser extraída, bem como a corrente de saturação de iónica, \(i^+_{sat}\) e o potencial flutuante \(V_f \), que deve ter um valor próximo do aquele que foi determinado empiricamente.
Usando os valores tabelados para a área da sonda e velocidade do som na iões do plasma, pode-se determinar a densidade electrónica do plasma. Visto que \(c_s = \sqrt{\dfrac{k T_e}{M}}\), e que a sonda tem \(10 mm \) de altura e um diâmetro de \(0.2 mm \) pode-se usar a \(i^+_{sat}\) para determinar a densidade.