Difference between revisions of "Angular Momentum Conservation"
| Line 55: | Line 55: | ||
[[File:Discos_velocidade_protocolo2.png|thumb|alt=|Figura2: rotational speed]] | [[File:Discos_velocidade_protocolo2.png|thumb|alt=|Figura2: rotational speed]] | ||
| − | [[File:Discos_tensao.png|thumb|alt=|Figura3: voltage across one of the resistors]] | + | [[File:Discos_tensao.png|thumb|alt=|Figura3: voltage across one |
| + | |||
| + | of the resistors]] | ||
[[File:Discos_tensao_compensada.png|thumb|alt=|Figura4: compensated voltage]] | [[File:Discos_tensao_compensada.png|thumb|alt=|Figura4: compensated voltage]] | ||
Revision as of 18:58, 13 October 2012
UNDER CONSTRUCTION
Contents
Description of the Experiment
This control room allows the confirmation of angular momentum conservation and the measuring of the moment of inertia of rotating discs.
Experimental Apparatus
The experimental apparatus is based in a PC hard-drive to which were added a servo and a group of discs that the servo keeps above the rotating discs. This setup allows the realization of the first protocol, centered in the study of angular momentum conservation.
The aparatus also has a group of braking resistors that can be connected in parallel with the motor windings. This setup allows the realization of the second protocol, centered in the study of the moment of inertia.
Protocol 1 - Angular Momentum Conservation
5 discs with a total mass of 115g are acelerated by the hard-drive motor until they reach 1500rpm. In this moment the motor is disconnected, the discs rotate freely and their speed is read. When a certain speed that the user defines previously is reached, the servo let's 3 suspended discs with a total mass of 69g initially at rest fall on top of the rotating discs.
In the end of the session a table is provided with the disc speed function of time, whose values will be used in a plot created in some program the user chooses.
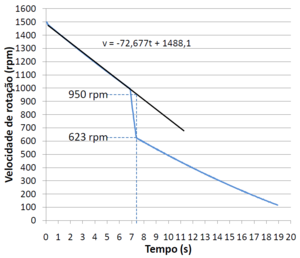
Figure1 is a plot created in Microsoft Excel using the table of results of an experience in which the servo let's the suspended discs fall when the discs below reach 1000 rpm.
Doing a linear regression between the deceleration and fall of the discs, it's possible to obtain the predicted rotational speed at the time that the falling discs stop sliding over the bottom discs.
Using the following quantities:
L - angular momentum
I - moment of inertia
ω - angular velocity
m - mass in rotation.
\[L_i=L_f\] \[I_i \omega_i=I_f \omega_f\] \[\frac{I_i}{I_f}=\frac{\omega_f}{\omega_i}\] \[\frac{\frac{m_i\left (r_1^2+r_2^2 \right )}{2}}{\frac{m_f\left (r_1^2+r_2^2 \right )}{2}}=\frac{\omega_f}{\omega_i}\] \[\frac{m_i}{m_f}=\frac{\omega_f}{\omega_i}\]
\[\frac{\omega_f}{\omega_i}=\frac{623}{950}=0,656\]
\[\frac{m_i}{m_f}=\frac{115}{115+69}=0,625\]
\[\frac{\left|0,656-0,625\right|}{\left|0,625\right|}\times 100=4,9\%\]
The speed ratio is different from the mass ratio by 4,9% which confirms the angular momentum conservation.
Protocol 2 - Moment of Inertia evaluation
5 discos com 115g no total são acelerados pelo motor do disco rígido até 1500rpm. Neste momento o motor desliga-se, os discos ficam a rodar livremente e a sua velocidade de rotação e tensão aos terminais de um dos enrolamentos vão sendo adquiridas. Quando for atingida uma velocidade escolhida previamente pelo utilizador, um relé coloca cada enrolamento do motor em paralelo com uma resistência com uma impedância igual à impedância do enrolamento. Estas resistências vão dissipar energia actuando como um travão electromagnético.
No final da sessão obtém-se uma tabela com a velocidade dos discos e tensão aos terminais de um enrolamento em função do tempo, cujos valores servirão para criar gráficos num programa ao critério do utilizador.
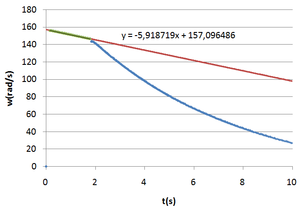
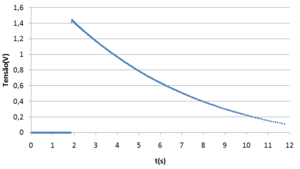
As Figuras 2 e 3 são gráficos criados no Microsoft Excel a partir da tabela de resultados de uma experiência em que o relé liga a 1000 rpm.
É evidente a diferença nos declives de desaceleração. Inicialmente é apenas o atrito cinético a desacelerar os discos, mas quando o relé liga, as resistências que são colocadas em paralelo com os enrolamentos do motor passam também a dissipar energia. A contribuição das resistências para a perda de velocidade e consequentemente de energia dos discos é dada pela diferença dos declives.
Quantificando:
\[\frac{d\omega_{res}}{dt}=\frac{d\omega_{atrito+res}}{dt}-\frac{d\omega_{atrito}}{dt}=-194,860-(-79,234)=-115,626rpm/s = -115,626\times\frac{2\pi}{60}=-12,11rad/s^2\]
É preciso descontar o declive do atrito também nas tensões, para a perda de energia nas resistências correspondente à perda de energia dada pela diferença dos declives de desaceleração dos discos. Pode-se para o efeito somar a função de ajuste da primeira série de dados da tensão à segunda série, fazer o gráfico do resultado e ajustar uma nova reta.
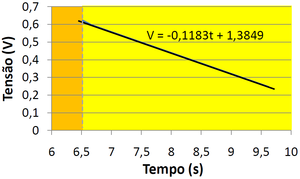
Para clarificar, somar-se-á 0,0241(t-6,42)V a cada ponto na tabela após o relé ligar e ajusta-se uma reta a essa série de dados. O resultado deste processo está apresentado na Figura4.
Utilizando a tensão dada pela reta de ajuste da Figura4 e sabendo que as resistências são de 5,3Ω chega-se à potência dissipada:
\[P=VI=V\frac{V}{R}=\frac{V^2}{R}\]
Integrando a potência dissipada obtém-se a energia dissipada nas 3 resistências:
\[\int_{6,67}^{9,62}\frac{dE}{dt}dt=3\int_{6,67}^{9,62}\frac{V^2}{R}dt=0,313J\]
A energia de um corpo rígido em rotação e a sua derivada no tempo são dadas por:
\[E=\frac{I\omega^2}{2}\;\;\;\;\;\;\;\;\;\;\frac{dE}{dt}=I\omega'\omega\]
Integra-se a última equação sabendo que \(\int_{6,67}^{9,62}\frac{dE}{dt}dt=-0,313J\) (coloca-se o "-" por se dissipar esta energia), ω' é constante = -12,11rad/s^2 (vem da diferença dos declives de desaceleração) e ω é dado pela reta de ajuste à desaceleração em rad/s,
\[\int_{6,67}^{9,62}\frac{dE}{dt}dt=\int_{6,67}^{9,62}I\omega'\omega \; dt\] \[-0,313=I(-12,11)\int_{6,67}^{9,62}\omega \; dt\] \[\frac{-0,313}{-12,11}=I\int_{6,67}^{9,62}-20,41t+230,93 dt\] \[I=\frac{-0,313}{-12,11\times 190,837}\] \[I=1,354\times 10^{-4}kg\, m^2\]
Ora, os discos desta experiência são na verdade coroas circulares de raios interior 13mm e exterior 47mm. O seu momento de inércia teórico corresponde então a:
\[I=\frac{m\left(r_1^2+r_2^2\right)}{2}=\frac{0,115\left(0,013^2+0,047^2\right)}{2}=1,367\times 10^{-4}kg \; m^2\]
Fazendo um desvio à exactidão,
\[\frac{\left|1,354\times 10^{-4}-1,367\times 10^{-4}\right|}{\left|1,367\times 10^{-4}\right|}\times 100=0,9\%\]
Conclui-se que esta experiência produziu resultados que se desviam dos calculados teoricamente por apenas 0,9%!!