Difference between revisions of "Lei de Boyle-Mariotte"
| Line 20: | Line 20: | ||
=Quem gosta desta iniciativa= | =Quem gosta desta iniciativa= | ||
| − | [[File: | + | [[File:EscolherCiencia.png|link=http://www.cienciaviva.pt/escolherciencia/|border|179px|border|179px]] |
| − | [[File:ECB Logo.png|link=http://www.externatobenedita.net/|border| | + | [[File:ECB Logo.png|link=http://www.externatobenedita.net/|border|179px|border|179px]] |
[[File:Logo_alberto_cores.jpg|link=http://www.es-al-berto.com/|border|120px|border|120px]] | [[File:Logo_alberto_cores.jpg|link=http://www.es-al-berto.com/|border|120px|border|120px]] | ||
[[File:LogoAEA_800x132.jpg|link=http://aealvalade.edu.pt/|border|240px|border|240px]] | [[File:LogoAEA_800x132.jpg|link=http://aealvalade.edu.pt/|border|240px|border|240px]] | ||
| Line 28: | Line 28: | ||
As escolas inicialmente envolvidas foram a Escola Secundária Padre António Vieira, Alvalade/Lisboa e o Externato Cooperativo da Benedita, Leiria. Também colaboraram nesta iniciativa a Escola Secundária Poeta Al Berto de Sines. | As escolas inicialmente envolvidas foram a Escola Secundária Padre António Vieira, Alvalade/Lisboa e o Externato Cooperativo da Benedita, Leiria. Também colaboraram nesta iniciativa a Escola Secundária Poeta Al Berto de Sines. | ||
| − | |||
=Aparato experimental= | =Aparato experimental= | ||
Revision as of 10:13, 25 February 2014
Contents
Descrição da experiência
O propósito desta experiência é a verificação da relação \( p \propto \frac{1}{V} \) (ou seja, que a pressão e o volume de um gás são inversamente proporcionais) durante uma compressão ou expansão isotérmica.
Ligações
- Video: rtsp://elabmc.ist.utl.pt/pv.sdp
- Laboratório: Básico em e-lab.ist.eu[1]
- Sala de controlo: pv
- Nivel: **
<swf height="270" width="510">http://www.elab.tecnico.ulisboa.pt/anexos/descricoes-flash/BoyleMariottePV.swf</swf>
Quem gosta desta iniciativa
Esta experiência encontra-se em duplicado no e-lab com seringas diferentes, estando uma delas alojada na Escola Secundária Padre António Vieira, em resultado do contrato PEC26 com a Ciência Viva - Agência Nacional para a Cultura Científica e Tecnológica. Este contrato visa por um lado (i) a partilha e a rentabilização de equipamentos de laboratório existente em escolas secundárias através da sua disponibilização on-line pela internet e por outro (ii) promover actividades de ensino experimental das ciências físicas. A automatização das experiências foi realizada por alunos do Técnico no âmbito do e-lab.
As escolas inicialmente envolvidas foram a Escola Secundária Padre António Vieira, Alvalade/Lisboa e o Externato Cooperativo da Benedita, Leiria. Também colaboraram nesta iniciativa a Escola Secundária Poeta Al Berto de Sines.
Aparato experimental
A montagem consiste num cilindro cheio de ar, cujo êmbolo é actuado por um servo motor (o par cilindro/êmbolo é implementado com uma seringa de 5cc).
É possível escolher os limites da compressão ou expansão do pistão e obter dados referentes ao curso do mesmo (volume) e da pressão a que se encontra o ar no interior do cilindro. A velocidade a que se desenrola a experiência também pode ser especificada escolhendo o tempo entre aquisições, podendo-se assim observar o desvio em relação à lei de Boyle-Mariotte se se escolher uma compressão ou expansão demasiado rápidas.
Protocolo
Os paramatros a definir são o volume inicial e final, o número de amostras e o tempo entre amostras.
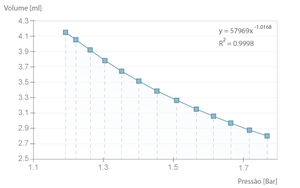
Se se executar a experiência com um tempo elevado entre amostras, estará a efectuar uma experiência isotérmica, ou seja, a temperatura do ar no êmbolo é aproximadamente constante e por isso a lei de Boyle-Mariotte verifica-se. O exemplo seguinte é um caso desses, onde se pode verificar que o produto \( pV \) é em média, \( 49,3 \pm 0,3 L.kPa \), aproximado ao valor teórico de \( nRT \) (considerando \( n = 2 \times 10 ^{-4} mol \), equivalente ao volume da seringa cheia e em repouso, ou seja \( 5 ml \), PTN).
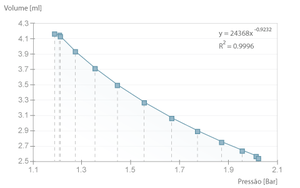
No caso de se diminuir o tempo entre amostras, o comportamento da compressão do ar deixa de ser isotérmico e passa a aproximar-se de adiabático, uma vez que não existe tempo para trocas de calor entre o ar no interior do cilindro e o meio ambiente. Desta forma a compressão afasta-se da lei de Boyle-Mariotte, claramente demonstrado pelo desvio da potência de ajuste, que no caso ideal seria \( ^3/_5 \) ( \( \gamma ^{-1} = \frac{c_v}{c_p} \) ). No entanto, é muito difícil obter uma rapidez de compressão que permita obter este valor, pois a termalização é muito rápida (dá-se na ordem da velocidade do som).
Protocolo Avançado
Com um tempo entre amostras elevado garantimos que a experiencia é isotérmica (ou seja, a temperatura mantém-se constante).
Nesta condição, são possíveis dois outros protocolos.
Volume fora da seringa
É possível determinar o valor do volume entre a seringa e os dispositivos associados, nomeadamente devido aos tubos que ligam ao sensor de pressão e à válvula de escape.
Considerando um volume \(V_0\) adicional ao volume da seringa, poderá proceder da seguinte forma:
- Efectue uma experiência com algumas aquisições (p. ex. 20), uma excursão máxima entre volume inicial e final e um tempo elevado entre amostras (situação da expansão isotérmica).
- Efectue um ajuste numérico considerando uma expressão do tipo \( p=a/(V+V_0)\) (utilizando o Fitteia ou o Origin p. ex.) aos dados experimentais onde a e V são parâmetros livres e determine \( V_0 \) e a constante de proporcionalidade \(a \) que será igual a \( nRT \).
Constante dos gases ideais
Considerando a temperatura da sala como sendo 22ºC podemos determinar R.
Procedimento:
- Fazer 20 aquisições com diferença máxima entre volumes (inicial e final) e tempo máximo entre amostras (isto aproxima-nos de uma transformação isotérmica).
- Ajustar os resultados a uma função do tipo \( a x ^b \) e encontrar a constante de proporcionalidade (que será \(a = nRT x\) ).
- Assumir que a temperatura da sala é 22ºC e determinar a quantidade de subtância presente dentro da seringa ( \(5 ml\) de ar em condições PTN). Determinar \( R \).
- Comparar este valor de \( R \) com a média do produto \( pV \) (ou seja, com software de cálculo matemático determinar o produto para cada linha e fazer a média).
- Fazer uma última estimativa de R fazendo uma ajuste a \( a x ^{-1} \).