Difference between revisions of "Conservação do Momento Angular"
| Line 4: | Line 4: | ||
=Aparato Experimental= | =Aparato Experimental= | ||
| − | O aparato experimental permite a realização | + | O aparato experimental consiste num disco rígido de computador ao qual foram adicionados um servo e um conjunto de discos suspensos por este. |
| + | Esta montagem permite a realização do primeiro protocolo experimental, centrado no estudo da conservação do momento angular. | ||
| + | |||
| + | O aparato conta ainda com um conjunto de resistências de travagem que podem ser colocadas em paralelo com os enrolamentos do motor do disco por um relé. | ||
| + | Esta montagem permite a realização do segundo protocolo experimental, centrado no estudo do momento de inércia. | ||
Cinco discos de um disco-duro dum PC com 115 g no total são acelerados a uma velocidade de 1500 rpm e depois deixados a rodar livremente; quando é atingida uma velocidade angular definida pelo utilizador, três discos com 69 g no total e com um diâmetro de 95 mm são deixados cair sobre os cinco anteriores. Sabendo que os discos têm as mesmas dimensões, verifique se há conservação do momento angular. | Cinco discos de um disco-duro dum PC com 115 g no total são acelerados a uma velocidade de 1500 rpm e depois deixados a rodar livremente; quando é atingida uma velocidade angular definida pelo utilizador, três discos com 69 g no total e com um diâmetro de 95 mm são deixados cair sobre os cinco anteriores. Sabendo que os discos têm as mesmas dimensões, verifique se há conservação do momento angular. | ||
Revision as of 10:56, 5 October 2012
Descrição da Experiência
Esta sala de controlo permite verificar a conservação do momento angular e medir o momento de inércia de um conjunto de discos em rotação.
Aparato Experimental
O aparato experimental consiste num disco rígido de computador ao qual foram adicionados um servo e um conjunto de discos suspensos por este. Esta montagem permite a realização do primeiro protocolo experimental, centrado no estudo da conservação do momento angular.
O aparato conta ainda com um conjunto de resistências de travagem que podem ser colocadas em paralelo com os enrolamentos do motor do disco por um relé. Esta montagem permite a realização do segundo protocolo experimental, centrado no estudo do momento de inércia.
Cinco discos de um disco-duro dum PC com 115 g no total são acelerados a uma velocidade de 1500 rpm e depois deixados a rodar livremente; quando é atingida uma velocidade angular definida pelo utilizador, três discos com 69 g no total e com um diâmetro de 95 mm são deixados cair sobre os cinco anteriores. Sabendo que os discos têm as mesmas dimensões, verifique se há conservação do momento angular.
Protocolo
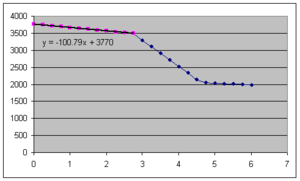
No exemplo da figura onde foram lançados os segundos discos a partir do instante 3 s, é efectuada uma regressão linear sobre os pontos iniciais antes de ocorrer o acoplamento dos discos. Obtida esta equação (p.ex. utilizando a função linha de tendência do Microsoft Excel) é possível extrapolar o que seria a velocidade no instante 5.5 s onde ambos os discos já rodam à mesma velocidade. Neste caso obter-se-ia uma velocidade de cerca de 3215 rpm. Consultando o valor na tabela para este instante, obstem-se uma leitura de 2010 rpm. A razão (2010/3215) deverá ser equivalente à razão das massas (3/5).
Protocolo Avançado
Esta experiência permite actuar um travão electromagnético que consiste em três resistências eléctricas que dissipam a energia gerada pelo motor a funcionar como gerador (tal como um dínamo de uma bicicleta). Este travão é actuado numa altura pré-determinada, o que origina uma forte desaceleração dos discos a partir desse instante. Comparando a desaceleração (variação da energia cinética de rotação) dos discos com a energia dissipada é possível estimar o momento de inércia I dos discos. O modo mais expedito consiste em integrar a potência dissipada, obtendo a energia dissipada ao longo do tempo; esta terá de ser igual à variação da energia cinética de rotação entre os instantes de integração considerados.
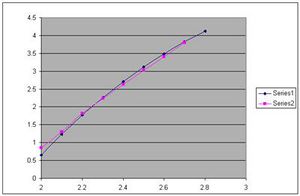
Gráfico do ajuste à serie 1 que representa a energia dissipada integrando a potência em função do tempo pela serie 2 obtida com o ajuste da função \[ E = \frac{I \omega ^2}{2} \] onde I é o parâmetro a ajustar. Com a definição do momento de inércia para um disco homogéneo presente: \[ I = \frac{m r ^2}{2} \] determina-o para a massa do raio do disco inicial e compara com o valor experimental obtido pelo balanço energético descrito no parágrafo anterior. É ainda interessante discutir qual a perda relativa de energia na colisão e se é possível afirmar que existe conservação do momento e da energia.