Difference between revisions of "Determinação da Constante de Planck"
m (→Protocolo) |
|||
| Line 14: | Line 14: | ||
# Identificar o ângulo para o qual ocorrem as várias riscas (cores) do espectro da lâmpada de mercúrio; | # Identificar o ângulo para o qual ocorrem as várias riscas (cores) do espectro da lâmpada de mercúrio; | ||
# Selecionar a risca pretendida e os filtros a utilizar para evitar a luz reflectida ou difundida de outros comprimentos de onda ou para atenuar a intensidade luminosa. | # Selecionar a risca pretendida e os filtros a utilizar para evitar a luz reflectida ou difundida de outros comprimentos de onda ou para atenuar a intensidade luminosa. | ||
| − | |||
| − | |||
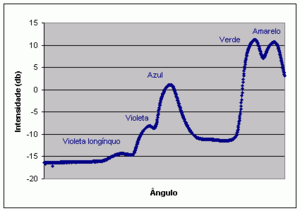
Para identificar as várias riscas deve ser efectuada a experiência em modo de varrimento. Neste modo, o gráfico do fototransistor permite determinar os ângulos para os quais existe luz. A ordem pelo qual ocorrem estes máximos é: | Para identificar as várias riscas deve ser efectuada a experiência em modo de varrimento. Neste modo, o gráfico do fototransistor permite determinar os ângulos para os quais existe luz. A ordem pelo qual ocorrem estes máximos é: | ||
| + | [[File:Plank-graph.png|thumb|alt=Gráfico da característica obtida pelo fototransistor onde é possível identificar os ângulos para os quais ocorrem as riscas da lâmpada de mercúrio.|Figura 1: Gráfico da característica obtida pelo fototransistor.]] | ||
{| border="1" style="text-align: center;" | {| border="1" style="text-align: center;" | ||
Revision as of 22:11, 26 May 2012
Contents
Descrição da Experiência
O objectivo desta experiência é o estudo do efeito foto-eléctrico num metal e a determinação da constante de Planck, uma vez que o efeito foto-elétrico é de natureza quântica.
Através da luz de uma lâmpada de mercúrio que é separada por uma rede de difracção nas suas riscas fundamentais (várias cores do espectro, tal como o arco-íris separa as cores da luz do Sol) é provocada a emissão de electrões numa célula foto-eléctrica para cada cor (comprimento de onda).
Aparato Experimental
Em construção.
Protocolo
Existem dois passos para atingir os objectivos propostos:
- Identificar o ângulo para o qual ocorrem as várias riscas (cores) do espectro da lâmpada de mercúrio;
- Selecionar a risca pretendida e os filtros a utilizar para evitar a luz reflectida ou difundida de outros comprimentos de onda ou para atenuar a intensidade luminosa.
Para identificar as várias riscas deve ser efectuada a experiência em modo de varrimento. Neste modo, o gráfico do fototransistor permite determinar os ângulos para os quais existe luz. A ordem pelo qual ocorrem estes máximos é:
| Cor | Frequência (s-1) | Comprimento de onda aproximado (nm) |
|---|---|---|
| Violeta longínquo | 8.22x1014 | 365 |
| Violeta | 7.41x1014 | 405 |
| Azul | 6.88x1014 | 436 |
| Verde | 5.49x1014 | 546 |
| Amarelo | 5.19x1014 | 578 |
Notas:
- A experiência desliga automaticamente a lâmpada de mercúrio ao fim de 30 min. Nessa situação é necessário esperar cerca de 15 minutos para estabilizar a potência da lâmpada após ser dado início à primeira experiência.
- A utilização do filtro de cor apropriado é importante para evitar a sobreposição de duas cores sobre a fotocélula que podem ocorrer por difusão da luz.
Determinação da constante de Planck
Efectuando a experiência no modo NORMAL poderá obter a característica temporal da carga de um condensador obtido pela corrente gerada na fotocélula. Quanto menor este tempo for maior será a corrente, significando que maior é a intensidade luminosa (como se demonstra no protocolo avançado).
- Pode observar cinco cores (riscas discretas principais correspondentes a transições entre níveis de energia discretos do átomo de Hg). Ajuste e seleccione o ângulo que pretender em função da cor.
- Para cada cor meça o potencial de paragem respectivo. Utilize os filtros amarelo e verde para as cores respectivas do espectro. Preencha uma tabela e use ângulos ligeiramente diferentes para estimar os erros da experiência.
- Faça o gráfico do potencial de paragem versus frequência.
Utilize um programa como por exemplo o EXCEL (opção “add trend line”/”adicionar linha de ajuste”) ou o ORIGIN para realizar o gráfico e para ajustar os dados por mínimos quadrados de modo a obter a constante de Planck e a “workfunction” (abcissa na origem). Não se esqueça de adicionar a coluna com o erro experimental e representá-lo no gráfico. Discuta os principais factores de erro que afectam a sua medida de h.
| Cor (1ª ordem) | Comprimento de onda (nm) | Frequência (x1014 Hz) | Potencial de paragem (V) |
|---|---|---|---|
| Amarelo | |||
| Verde | |||
| Azul | |||
| Violeta | |||
| Violeta 2 |
Protocolo Avançado
O modelo clássico da radiação e o modelo corpuscular
De acordo com a teoria corpuscular da luz (“a luz são fotões”) a energia máxima dos foto-electrões no efeito foto-eléctrico depende apenas da frequência da luz incidente e é independente da sua intensidade e dependente do comprimento de onda. No modelo clássico (“a luz são ondas”) a energia cinética dos foto-electrões depende da intensidade da luz incidente. Quanto maior a intensidade, ou seja a amplitude da onda, maior a sua energia. Vamos verificar qual das hipóteses é mais correcta:
- Escolha uma das cores sobre a célula foto-eléctrica (no caso do amarelo ou verde utilize os filtros respectivos).
- Coloque o filtro neutro de intensidade variável em frente do reflector de modo que a luz passe pela zona dos 100% de transmissão. Tome nota da tensão de paragem. Determine o tempo necessário para voltar a obter a tensão máxima, ignorando o transitório do início da experiência.
- Repita os passos anteriores, mas para as outras posições do filtro neutro correspondentes a uma intensidade diferente, para a mesma frequência de luz incidente.
- Repita estes passos para uma nova cor do espectro.
- Compare o efeito de variar a intensidade da luz incidente para uma mesma frequência, no potencial de paragem, com o efeito de variar o comprimento de onda para uma mesma intensidade. Esta experiência comprova o modelo clássico(ondulatório) ou corpuscular para a luz?
| Cor #1 __________(nome) | Transmissão (%) | Potencial paragem (V) | Tempo de carga (s) |
|---|---|---|---|
| 100 | |||
| 80 | |||
| 60 | |||
| 40 | |||
| 20 | |||
| Cor #2 __________(nome) | Transmissão (%) | Potencial paragem (V) | Tempo de carga (s) |
| 100 | |||
| 80 | |||
| 60 | |||
| 40 | |||
| 20 |
Princípios Teóricos
Efeito Fotoeléctrico
O efeito foto-eléctrico consiste na emissão de electrões da superfície de um metal quando este é iluminado por luz de uma dada frequência (\( \nu \)). Um fotão de energia \( E = h \nu \) ao incidir no metal transfere a sua energia a um electrão pertencente a um dos átomos na rede cristalina do metal. A emissão de electrões do metal é muito dependente da frequência da luz incidente. Para cada metal, existe uma frequência critica, \( \nu _0 \), tal que para luz incidente com frequência inferior não há foto-electrões arrancados. Por outro lado, para frequências superiores, a energia dos foto-electrões emitidos aumenta linearmente com a energia dos fotões incidentes. A intensidade da luz incidente afecta somente o número de foto-electrões emitidos, mas não a sua energia, contrariamente ao que seria de esperar na teoria clássica da radiação. Einstein propôs a seguinte explicação para o fenómeno: a luz é transportada por fotões com uma dada energia E associada à frequência da luz \( \nu \):
\[ E = h \times \nu \]
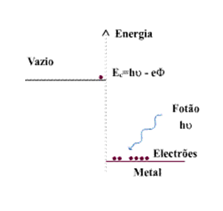
em que h é a constante de Planck. O efeito foto-eléctrico deve-se a uma colisão do fotão com o electrão, em que aquele transmite a este toda a sua energia. Tendo em conta que a energia de um electrão no vazio e dentro do metal é diferente (mais elevada no vazio), só se verifica efeito foto-eléctrico se a energia transmitida pelo fotão for superior à diferença entre estas duas energias (ver Fig. 1). Assim, a energia com que o electrão abandona o metal é igual à energia do fotão menos a energia "gasta" para o electrão abandonar o metal:
\[ E = h \times \nu - e \times \phi, \]
em que e é a carga do electrão e \( \phi \) é a diferença de workfunction. Tal como foi anteriormente enunciado, à medida que a frequência da luz incidente decresce, os fotões têm menos energia, e a partir de uma frequência critica \( \nu _0 \) não são emitidos mais foto-electrões. Neste caso, \( E _{max} = 0 \) e da Eq. l tiramos
\[ h \nu _0 = e \phi \quad ou \quad \nu _0 = \frac{e}{h} \phi \]
Efeito Fotoeléctrico
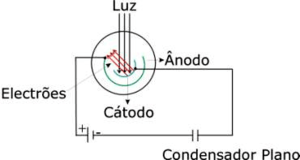
Uma célula foto-eléctrica é um dispositivo onde a luz incidente sobre uma superfície metálica (cátodo) excita electrões que vão ser colectados numa superfície metálica concêntrica (ânodo), tal como exemplificado na figura, e que na prática é um condensador semi-cilíndrico de capacidade muito baixa. Ligando o ânodo e o cátodo por um circuito externo, podemos medir a corrente produzida pelos foto-electrões. No caso mais genérico, a energia cinética máxima dos foto-electrões emitidos é determinada aplicando um potencial de paragem, Vc entre o ânodo e o cátodo de modo a impedir que os foto-electrões emitidos pelo cátodo atinjam o ânodo. Deste modo, deixa de fluir corrente no circuito.
A célula inicialmente tem aplicada a tensão da fonte, aproximadamente 9V uma vez que o condensador é descarregado no início da experiência (é efectuado um curto-circuito aos seus terminais). Como a célula está em série com o condensador, este vai carregando à medida que são gerados foto-electrões, criando uma corrente eléctrica no circuito que atravessa a célula. À medida que o condensador carrega, aumenta a diferença de potencial aos seus terminais, o que obriga a diminuir a tensão aos terminais da célula (note que \( V_{bat} = V_{Cond} + V_{célula} = constante \)). Quando a diferença de potencial nas placas da célula for igual a \( V_c = \frac{h \times \nu - e \times \phi}{e} \), deixa de fluir corrente no circuito e o condensador passa a ter uma tensão constante aos seus terminais.
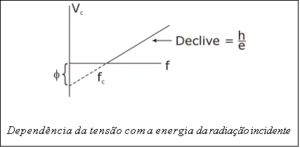
Conhecendo dois ou mais valores dessa tensão para determinadas frequências [1] pode-se efectuar uma regressão linear e determinar não só \( \phi \) mas também a constante de Planck. No gráfico seguinte esquematizamos a dependência da tensão de paragem V em função da frequência da luz incidente para um dado metal. A função em causa corresponde a uma recta de declive \( \frac{h}{e} \) e coeficiente na origem \( \phi \).
Elementos Históricos
Em 1921 foi atribuído a Albert Einstein o Prémio Nobel da Física pelas suas descobertas no efeito fotoeléctrico.