Difference between revisions of "Angular Momentum Conservation"

From wwwelab
Jump to navigation Jump to search
m (Text replacement - "|left" to "|center")
 
(80 intermediate revisions by 4 users not shown)
Line 1: Line 1:
−
UNDER CONSTRUCTION
+
=Description of the Experiment=
 +
This control room allows the confirmation of angular momentum conservation by making collide a spinning disk with another one. Beyond that, the disk inertia momentum can be extrapolated based on the principles of conservation of energy.
 +
 
 +
<!-- Acho que este texto não está muito correcto. -->
 +
 
 +
 
 +
<div class="toccolours mw-collapsible mw-collapsed" style="width:420px">
 +
'''Links'''
 +
<div class="mw-collapsible-content">
 +
 
 +
*Video: rtsp://elabmc.ist.utl.pt/inertiadisks.sdp
 +
*Laboratory: Intermediate in [http://e-lab.ist.eu e-lab.ist.eu]
 +
*Control room: [unavaliable]
 +
*Level: ***
 +
 
 +
</div>
 +
</div>
 +
 
 +
{{#ev:youtube|X2OK3akY4GE|Slow motion video (12x) of the discs connecting.|center}}
  
−
=Description of the Experiment=
 
−
This control room allows the confirmation of angular momentum conservation and the measuring of the moment of inertia of rotating discs.
 
  
 
=Experimental Apparatus=
 
=Experimental Apparatus=
−
The experimental apparatus is based in a PC hard-drive to which were added a servo and a group of discs that the servo keeps above the rotating discs. This setup allows the realization of the first protocol, centered in the study of angular momentum conservation.
+
The experimental apparatus is based on a PC hard disk drive motor and its spinning disc with a mass of 115g, 12.5mm internal radius and 47.5mm external. A second disc with a mass of 69g and the same dimensions is held on top of it and can be dropped by a servo motor actuator.
 +
 
 +
The motor of the apparatus can be used as a generator equipped with a switchable resistor, acting as an electromagnetic brake. The braking current and the voltage characteristic are measured allowing an accurate calculation of energy dissipation.
 +
 
  
−
The aparatus also has a group of braking resistors that can be connected in parallel with the motor windings. This setup allows the realization of the second protocol, centered in the study of the moment of inertia.
+
=Protocol - Angular Momentum Conservation=
  
−
=Protocol1 - Angular Momentum Conservation=
+
[[File:Discs_velocity_protocol1.png|thumb|alt=|Figure 1: Angular velocity (rpm) as a function of time for a collision at 1000 rpm.]]
  
−
[[File:Discos_velocidade_protocolo1.png|thumb|alt=|Figura1: rotational speed]]
+
The bottom disc is accelerated by the motor until it reaches a selected angular velocity. At this point, the engine is disconnected from power and the disc is allowed to rotate freely. When a certain pre-determined velocity is reached, the servo lets the suspended disc initially at rest fall on top of the rotating disc.
  
−
5 discs with a total mass of 115g are acelerated by the hard-drive motor until they reach 1500rpm. In this moment the motor is disconnected, the discs rotate freely and their speed is read. When a certain speed that the user defines previously is reached, the servo let's 3 suspended discs with a total mass of 69g initially at rest fall on top of the rotating discs.
+
Data taken from the experiment is given and plotted with the disc velocity in function of time.
  
−
In the end of the session a table is provided with the disc speed function of time, whose values will be used in a plot created in some program the user chooses.
+
'''Figure1''' is a plot of the results of an experiment in which a servo lets the suspended disc fall when the disc below reaches 1000 rpm.
  
−
'''Figure1''' is a plot created in Microsoft Excel using the table of results of an experience in which the servo let's the suspended discs fall when the discs below reach 1000 rpm.  
+
Doing a linear regression between the deceleration and the fall of the disc, it is possible to obtain the predicted velocity at any time. This gives us the rule of thumb of the friction deceleration related to angular velocity.
  
−
Doing a linear regression between the deceleration and fall of the discs, it's possible to obtain the predicted rotational speed at the time that the falling discs stop sliding over the bottom discs.
 
  
−
Using the following quantities:
+
=Advanced Protocol - Moment of Inertia Evaluation=
 +
 
 +
[[File:Discos_velocidade_protocolo2.png|thumb|alt=|Figure2: Rotational velocity as function of time after the electromagnetic breaking.|right|border|240px]]
 +
[[File:Discos_tensao_2fases.png|thumb|alt=|Figure3: Circuit schematic for voltage measurement.|right|border|240px]]
 +
[[File:Discos_tensao.png|thumb|alt=|Figure4: Voltage between two phases during breaking.|right|border|240px]]
 +
[[File:W_extrap.gif|thumb|alt=|Figure5: Extrapolation of w based on the initial slope of deceleration.|right|border|240px]]
 +
[[File:Discos_balanco_energetico.png|thumb|alt=|Figure6: Final energy balance showing electrical and mechanical component allowing you to get the total moment of inertia.|right|border|240px]]
 +
 
 +
The bottom disc is accelerated by the motor to a selected angular velocity. At that time the motor supply is disconnected and the disc is allowed to rotate freely. When a certain pre-determined velocity is reached, a relay puts each motor winding in parallel with a resistor  resistance similar to the windings of the motor  ('''Picture 3'''). These resistors will dissipate energy, acting as an electromagnetic brake. Voltage and velocity as functions of time are given in a table of results at the end of the session.
 +
 
 +
'''Figures 2''' and '''4''' are plots obtained through the table of results of an experiment in which the relay turns on when the rotating discs reach 1400 rpm.
 +
 
 +
Using the first data from '''Figure 2''', before the braking, to do a linear regression, you can get the angular deceleration caused by friction, assumed constant all the time, from the slope of the line. From this deceleration it will be possible to calculate  the instantaneous loss of angular momentum deferentially.
 +
 
 +
Between each speed acquisition an energy balance is done . The loss of total mechanical energy must be equal to the sum of losses by friction and electromagnetic breaking.
 +
 
 +
<math>  \Delta E_{mec} = \Delta E_{friction} + \Delta E_{elec}</math>
 +
 
 +
The energy of a rotating body is <math> E_{rot}=\frac{I w^2}{2}</math> I being the moment of inertia. Then, the variation of mechanical energy between each acquisition will be:
 +
 
 +
<math>\Delta E_{mec}=\frac{I(w_{n+1}^2-w_{n}^2)}{2}</math>
 +
 
 +
<math>w_{n+1}</math> and <math>w_{n}</math> being the angular velocity in two consecutive acquisitions.
 +
 
 +
Using the initial slope of deceleration <math>a</math> due to mechanical friction, one can extrapolate <math>w_{n+1}</math> in absence of electromagnetic breaking.
 +
 
 +
<math>w_{n+1}= w_{n} + a \Delta t</math>
 +
 
 +
Substituting this extrapolated <math>w_{n+1}</math> in the equation of total energy variation it is possible to calculate the energy dissipation due to mechanical friction:
 +
 
 +
<math>\Delta E_{friction}=\frac{I(w_{n}^2+2w_{n}a\Delta t + a^2\Delta t^2-w_{n}^2)}{2}</math>
 +
 
 +
<math>\Delta E_{friction}=\frac{I(2w_{n}a\Delta t + a^2\Delta t^2)}{2}</math>
 +
 
 +
A set of extrapolations of <math>w_{n+1}</math> can be seen in '''Figure 5'''.
 +
 
 +
The dissipated power is:
 +
 
 +
<math>P=VI=\frac{V^2}{R}</math>
 +
 
 +
The rms voltage across one winding is:
 +
 
 +
<math>V_{rms}=\frac{V_{measured}}{\sqrt{3}\sqrt{2}}</math>
 +
 
 +
In the setup used, the energy dissipates in 3 branches, so the power comes multiplied by 3.  Besides, each winding is in parallel with a resistor with the same resistance value <math>4,7\Omega</math>, which means the power equation will come multiplied by 2 and <math>R=4,7\Omega</math> will be used.
 +
 
 +
<math>P=3\times2\times\frac{V_{rms}^2}{R}=3\times2\times\left(\frac{V_{measured}}{\sqrt{3}\sqrt{2}}\right)^2\frac{1}{R}</math>
 +
 
 +
<math>P=\frac{V^2}{R}</math>
 +
 
 +
The energy dissipated will be:
 +
 
 +
<math>\Delta E_{ele}=P*\Delta t</math>
  
−
L - angular momentum
+
Where <math>\Delta t</math> is the time between acquisitions.
  
−
I - moment of inertia
+
The ballance between each consecutive acquitition is summed in the end.
  
−
&omega; - angular velocity
+
<math>Balance = \Delta E_{mec} - \Delta E_{friction} - \Delta E_{elec}</math>
  
−
m - mass in rotation.
+
Finally the goal-seek function of Microsoft Excel is used to force the sum of balances to be 0 (zero) changing the value of I.
  
−
<div style="text-align: center;">We have for the angular momentum conservation:</div>
+
Using this method, we reached an experimental value of <math>1,274\times10^{-4} kg m^2</math>  for the moment of inertia.
−
\[L_i=L_f\]
 
−
\[I_i \omega_i=I_f \omega_f\]
 
−
\[\frac{I_i}{I_f}=\frac{\omega_f}{\omega_i}\]
 
−
\[\frac{\frac{m_i\left (r_1^2+r_2^2 \right )}{2}}{\frac{m_f\left (r_1^2+r_2^2 \right )}{2}}=\frac{\omega_f}{\omega_i}\]
 
−
\[\frac{m_i}{m_f}=\frac{\omega_f}{\omega_i}\]
 
  
−
<div style="text-align: center;">The experimental results give:</div>
+
'''Figure 6''' shows the energy of the disc in function of time, the energy lost by friction and electromagnetic breaking and the sum of all the energies that allows the verification of the conservation of energy throughout the experiment.
  
−
\[\frac{\omega_f}{\omega_i}=\frac{623}{950}=0,656\]
+
The disc is in fact a ring having an interior radius of 13mm and an exterior radius of 47mm, so its theoretical moment of inertia is:
  
−
<div style="text-align: center;">while the predicted mass ratio is</div>
+
<math>I=\frac{m\left(r_1^2+r_2^2\right)}{2}=\frac{0,115\left(0,013^2+0,047^2\right)}{2}=1,367\times 10^{-4}kg \; m^2</math>
  
−
\[\frac{m_i}{m_f}=\frac{115}{115+69}=0,625\]
+
Evaluating the accuracy:
  
−
<div style="text-align: center;">Evaluating the accuracy</div>
+
<math>\frac{\left|1,274\times 10^{-4}-1,367\times 10^{-4}\right|}{\left|1,367\times 10^{-4}\right|}\times 100=6,8\%</math>
  
−
\[\frac{\left|0,656-0,625\right|}{\left|0,625\right|}\times 100=4,9\%\]
+
This experiment gave results that differ by '''6,8%''' from the ones calculated theoretically.
  
−
The speed ratio is different from the mass ratio by 4,9% which confirms the angular momentum conservation.
+
=Physics=
 +
Using the following quantities:
  
−
=Protocolo 2 - Medição do Momento de Inércia=
+
L - angular momentum
  
−
[[File:Discos_velocidade_protocolo2.png|thumb|alt=|Figura2: velocidade de rotação]]
+
I - moment of inertia
−
[[File:Discos_tensao.png|thumb|alt=|Figura3: tensão numa das&nbsp;resistências]]
 
−
[[File:Discos_tensao_compensada.png|thumb|alt=|Figura4: tensão compensada]]
 
  
−
5 discos com 115g no total são acelerados pelo motor do disco rígido até 1500rpm. Neste momento o motor desliga-se, os discos ficam a rodar livremente e a sua velocidade de rotação e tensão aos terminais de um dos enrolamentos vão sendo adquiridas. Quando for atingida uma velocidade escolhida previamente pelo utilizador, um relé coloca cada enrolamento do motor em paralelo com uma resistência com uma impedância igual à impedância do enrolamento. Estas resistências vão dissipar energia actuando como um travão electromagnético.
+
&omega; - angular velocity
 +
 
 +
m - mass in rotation.
  
−
No final da sessão obtém-se uma tabela com a velocidade dos discos e tensão aos terminais de um enrolamento em função do tempo, cujos valores servirão para criar gráficos num programa ao critério do utilizador.
+
For the angular momentum conservation:
  
−
As '''Figuras 2''' e '''3''' são gráficos criados no Microsoft Excel a partir da tabela de resultados de uma experiência em que o relé liga a 1000 rpm.
+
<math>L_i=L_f</math>
  
−
É evidente a diferença nos declives de desaceleração. Inicialmente é apenas o atrito cinético a desacelerar os discos, mas quando o relé liga, as resistências que são colocadas em paralelo com os enrolamentos do motor passam também a dissipar energia. A contribuição das resistências para a perda de velocidade e consequentemente de energia dos discos é dada pela diferença dos declives.
+
<math>I_i \omega_i=I_f \omega_f</math>
  
−
Quantificando:
+
<math>\frac{I_i}{I_f}=\frac{\omega_f}{\omega_i}</math>
  
−
\[\frac{d\omega_{res}}{dt}=\frac{d\omega_{atrito+res}}{dt}-\frac{d\omega_{atrito}}{dt}=-194,860-(-79,234)=-115,626rpm/s = -115,626\times\frac{2\pi}{60}=-12,11rad/s^2\]
+
<math>\frac{\frac{m_i\left (r_1^2+r_2^2 \right )}{2}}{\frac{m_f\left (r_1^2+r_2^2 \right )}{2}}=\frac{\omega_f}{\omega_i}</math>
  
−
É preciso descontar o declive do atrito também nas tensões, para a perda de energia nas resistências correspondente à perda de energia dada pela diferença dos declives de desaceleração dos discos. Pode-se para o efeito somar a função de ajuste da primeira série de dados da tensão à segunda série, fazer o gráfico do resultado e ajustar uma nova reta.
+
<math>\frac{m_i}{m_f}=\frac{\omega_f}{\omega_i}</math>
  
−
Para clarificar, somar-se-á 0,0241(t-6,42)V a cada ponto na tabela após o relé ligar e ajusta-se uma reta a essa série de dados. O resultado deste processo está apresentado na '''Figura4'''.
+
The experimental results give:
  
−
Utilizando a tensão dada pela reta de ajuste da '''Figura4''' e sabendo que as resistências são de 5,3&Omega; chega-se à potência dissipada:
+
<math>\frac{\omega_f}{\omega_i}=\frac{623}{950}=0,656</math>
  
−
\[P=VI=V\frac{V}{R}=\frac{V^2}{R}\]
+
while the predicted mass ratio is
  
−
Integrando a potência dissipada obtém-se a energia dissipada nas 3 resistências:
+
<math>\frac{m_i}{m_f}=\frac{115}{115+69}=0,625</math>
  
−
\[\int_{6,67}^{9,62}\frac{dE}{dt}dt=3\int_{6,67}^{9,62}\frac{V^2}{R}dt=0,313J\]
+
Evaluating the accuracy:
  
−
A energia de um corpo rígido em rotação e a sua derivada no tempo são dadas por:
+
<math>\frac{\left|0,656-0,625\right|}{\left|0,625\right|}\times 100=4,9\%</math>
  
−
\[E=\frac{I\omega^2}{2}\;\;\;\;\;\;\;\;\;\;\frac{dE}{dt}=I\omega'\omega\]
+
The speed ratio is different from the mass ratio by 4,9%, which gives a good approximation of the angular momentum conservation.
  
−
Integra-se a última equação sabendo que \(\int_{6,67}^{9,62}\frac{dE}{dt}dt=-0,313J\) (coloca-se o "-" por se dissipar esta energia), &omega;' é constante = -12,11rad/s^2 (vem da diferença dos declives de desaceleração) e &omega; é dado pela reta de ajuste à desaceleração em rad/s,
+
Knowing the exact dimensions of the disks (<math>r_1=12,5mm, r_2=47,5mm</math>) and adding an error momentum to the equations, you can infer an approximated value of the motor rotor momentum of inertia (or its mass knowing its average radius).
  
−
\[\int_{6,67}^{9,62}\frac{dE}{dt}dt=\int_{6,67}^{9,62}I\omega'\omega \; dt\]
+
<math>I_i \omega_i=I_f \omega_f</math>
−
\[-0,313=I(-12,11)\int_{6,67}^{9,62}\omega \; dt\]
 
−
\[\frac{-0,313}{-12,11}=I\int_{6,67}^{9,62}-20,41t+230,93 dt\]
 
−
\[I=\frac{-0,313}{-12,11\times 190,837}\]
 
−
\[I=1,354\times 10^{-4}kg\, m^2\]
 
  
−
Ora, os discos desta experiência são na verdade coroas circulares de raios interior 13mm e exterior 47mm. O seu momento de inércia teórico corresponde então a:
+
<math>\left (I_m + I_{Di}\right ) \omega_i=\left (I_m + I_{Df}\right ) \omega_f</math>
  
−
\[I=\frac{m\left(r_1^2+r_2^2\right)}{2}=\frac{0,115\left(0,013^2+0,047^2\right)}{2}=1,367\times 10^{-4}kg \; m^2\]
+
Solving in for <math>I_m</math>
  
−
Fazendo um desvio à exactidão,
+
<math>I_m = \frac{I_{Df} \omega_f - I_{Di} \omega_i}{\omega_i-\omega_f}</math>
  
−
\[\frac{\left|1,354\times 10^{-4}-1,367\times 10^{-4}\right|}{\left|1,367\times 10^{-4}\right|}\times 100=0,9\%\]
 
  
−
Conclui-se que esta experiência produziu resultados que se desviam dos calculados teoricamente por apenas '''0,9%'''!!
+
=Links=
 +
*[[Conservação do Momento Angular | Portuguese version (Versão em Português)]]

Latest revision as of 14:12, 28 May 2015

Description of the Experiment

This control room allows the confirmation of angular momentum conservation by making collide a spinning disk with another one. Beyond that, the disk inertia momentum can be extrapolated based on the principles of conservation of energy.


Links

  • Video: rtsp://elabmc.ist.utl.pt/inertiadisks.sdp
  • Laboratory: Intermediate in e-lab.ist.eu
  • Control room: [unavaliable]
  • Level: ***


Experimental Apparatus

The experimental apparatus is based on a PC hard disk drive motor and its spinning disc with a mass of 115g, 12.5mm internal radius and 47.5mm external. A second disc with a mass of 69g and the same dimensions is held on top of it and can be dropped by a servo motor actuator.

The motor of the apparatus can be used as a generator equipped with a switchable resistor, acting as an electromagnetic brake. The braking current and the voltage characteristic are measured allowing an accurate calculation of energy dissipation.


Protocol - Angular Momentum Conservation

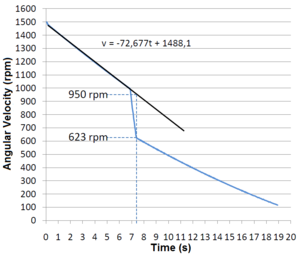
Figure 1: Angular velocity (rpm) as a function of time for a collision at 1000 rpm.

The bottom disc is accelerated by the motor until it reaches a selected angular velocity. At this point, the engine is disconnected from power and the disc is allowed to rotate freely. When a certain pre-determined velocity is reached, the servo lets the suspended disc initially at rest fall on top of the rotating disc.

Data taken from the experiment is given and plotted with the disc velocity in function of time.

Figure1 is a plot of the results of an experiment in which a servo lets the suspended disc fall when the disc below reaches 1000 rpm.

Doing a linear regression between the deceleration and the fall of the disc, it is possible to obtain the predicted velocity at any time. This gives us the rule of thumb of the friction deceleration related to angular velocity.


Advanced Protocol - Moment of Inertia Evaluation

Figure2: Rotational velocity as function of time after the electromagnetic breaking.
Figure3: Circuit schematic for voltage measurement.
Figure4: Voltage between two phases during breaking.
Figure5: Extrapolation of w based on the initial slope of deceleration.
Figure6: Final energy balance showing electrical and mechanical component allowing you to get the total moment of inertia.

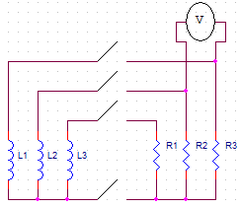
The bottom disc is accelerated by the motor to a selected angular velocity. At that time the motor supply is disconnected and the disc is allowed to rotate freely. When a certain pre-determined velocity is reached, a relay puts each motor winding in parallel with a resistor resistance similar to the windings of the motor (Picture 3). These resistors will dissipate energy, acting as an electromagnetic brake. Voltage and velocity as functions of time are given in a table of results at the end of the session.

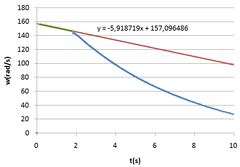
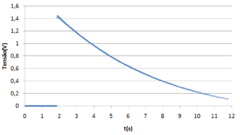
Figures 2 and 4 are plots obtained through the table of results of an experiment in which the relay turns on when the rotating discs reach 1400 rpm.

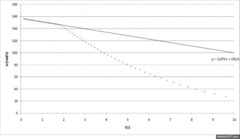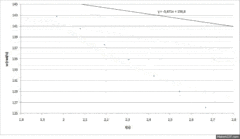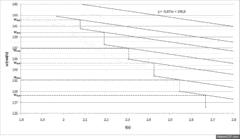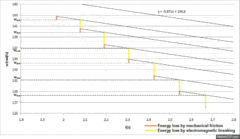
Using the first data from Figure 2, before the braking, to do a linear regression, you can get the angular deceleration caused by friction, assumed constant all the time, from the slope of the line. From this deceleration it will be possible to calculate the instantaneous loss of angular momentum deferentially.

Between each speed acquisition an energy balance is done . The loss of total mechanical energy must be equal to the sum of losses by friction and electromagnetic breaking.

[math] \Delta E_{mec} = \Delta E_{friction} + \Delta E_{elec}[/math]

The energy of a rotating body is [math] E_{rot}=\frac{I w^2}{2}[/math] I being the moment of inertia. Then, the variation of mechanical energy between each acquisition will be:

[math]\Delta E_{mec}=\frac{I(w_{n+1}^2-w_{n}^2)}{2}[/math]

[math]w_{n+1}[/math] and [math]w_{n}[/math] being the angular velocity in two consecutive acquisitions.

Using the initial slope of deceleration [math]a[/math] due to mechanical friction, one can extrapolate [math]w_{n+1}[/math] in absence of electromagnetic breaking.

[math]w_{n+1}= w_{n} + a \Delta t[/math]

Substituting this extrapolated [math]w_{n+1}[/math] in the equation of total energy variation it is possible to calculate the energy dissipation due to mechanical friction:

[math]\Delta E_{friction}=\frac{I(w_{n}^2+2w_{n}a\Delta t + a^2\Delta t^2-w_{n}^2)}{2}[/math]

[math]\Delta E_{friction}=\frac{I(2w_{n}a\Delta t + a^2\Delta t^2)}{2}[/math]

A set of extrapolations of [math]w_{n+1}[/math] can be seen in Figure 5.

The dissipated power is:

[math]P=VI=\frac{V^2}{R}[/math]

The rms voltage across one winding is:

[math]V_{rms}=\frac{V_{measured}}{\sqrt{3}\sqrt{2}}[/math]

In the setup used, the energy dissipates in 3 branches, so the power comes multiplied by 3. Besides, each winding is in parallel with a resistor with the same resistance value [math]4,7\Omega[/math], which means the power equation will come multiplied by 2 and [math]R=4,7\Omega[/math] will be used.

[math]P=3\times2\times\frac{V_{rms}^2}{R}=3\times2\times\left(\frac{V_{measured}}{\sqrt{3}\sqrt{2}}\right)^2\frac{1}{R}[/math]

[math]P=\frac{V^2}{R}[/math]

The energy dissipated will be:

[math]\Delta E_{ele}=P*\Delta t[/math]

Where [math]\Delta t[/math] is the time between acquisitions.

The ballance between each consecutive acquitition is summed in the end.

[math]Balance = \Delta E_{mec} - \Delta E_{friction} - \Delta E_{elec}[/math]

Finally the goal-seek function of Microsoft Excel is used to force the sum of balances to be 0 (zero) changing the value of I.

Using this method, we reached an experimental value of [math]1,274\times10^{-4} kg m^2[/math] for the moment of inertia.

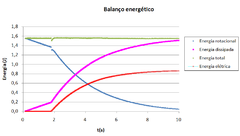
Figure 6 shows the energy of the disc in function of time, the energy lost by friction and electromagnetic breaking and the sum of all the energies that allows the verification of the conservation of energy throughout the experiment.

The disc is in fact a ring having an interior radius of 13mm and an exterior radius of 47mm, so its theoretical moment of inertia is:

[math]I=\frac{m\left(r_1^2+r_2^2\right)}{2}=\frac{0,115\left(0,013^2+0,047^2\right)}{2}=1,367\times 10^{-4}kg \; m^2[/math]

Evaluating the accuracy:

[math]\frac{\left|1,274\times 10^{-4}-1,367\times 10^{-4}\right|}{\left|1,367\times 10^{-4}\right|}\times 100=6,8\%[/math]

This experiment gave results that differ by 6,8% from the ones calculated theoretically.

Physics

Using the following quantities:

L - angular momentum

I - moment of inertia

ω - angular velocity

m - mass in rotation.

For the angular momentum conservation:

[math]L_i=L_f[/math]

[math]I_i \omega_i=I_f \omega_f[/math]

[math]\frac{I_i}{I_f}=\frac{\omega_f}{\omega_i}[/math]

[math]\frac{\frac{m_i\left (r_1^2+r_2^2 \right )}{2}}{\frac{m_f\left (r_1^2+r_2^2 \right )}{2}}=\frac{\omega_f}{\omega_i}[/math]

[math]\frac{m_i}{m_f}=\frac{\omega_f}{\omega_i}[/math]

The experimental results give:

[math]\frac{\omega_f}{\omega_i}=\frac{623}{950}=0,656[/math]

while the predicted mass ratio is

[math]\frac{m_i}{m_f}=\frac{115}{115+69}=0,625[/math]

Evaluating the accuracy:

[math]\frac{\left|0,656-0,625\right|}{\left|0,625\right|}\times 100=4,9\%[/math]

The speed ratio is different from the mass ratio by 4,9%, which gives a good approximation of the angular momentum conservation.

Knowing the exact dimensions of the disks ([math]r_1=12,5mm, r_2=47,5mm[/math]) and adding an error momentum to the equations, you can infer an approximated value of the motor rotor momentum of inertia (or its mass knowing its average radius).

[math]I_i \omega_i=I_f \omega_f[/math]

[math]\left (I_m + I_{Di}\right ) \omega_i=\left (I_m + I_{Df}\right ) \omega_f[/math]

Solving in for [math]I_m[/math]

[math]I_m = \frac{I_{Df} \omega_f - I_{Di} \omega_i}{\omega_i-\omega_f}[/math]


Links

Retrieved from "http://www.elab.tecnico.ulisboa.pt/wiki/index.php?title=Angular_Momentum_Conservation&oldid=1715"