Difference between revisions of "Estatística de Dados"
| Line 118: | Line 118: | ||
| − | <div class="toccolours mw-collapsible mw-collapsed" style="width: | + | <div class="toccolours mw-collapsible mw-collapsed" style="width:600px"> |
'''Estudo da frequância ideal para excitar os dados''' | '''Estudo da frequância ideal para excitar os dados''' | ||
<div class="mw-collapsible-content"> | <div class="mw-collapsible-content"> | ||
| Line 245: | Line 245: | ||
| 0.0491 | | 0.0491 | ||
|} | |} | ||
| + | |||
De notar que, regra geral, as trajectórias cruzam-se perto do mínimo da trajectória da plataforma (cos(2pf t ) >> -1), já quando esta vai a subir (-sin(2p f t ) >0). | De notar que, regra geral, as trajectórias cruzam-se perto do mínimo da trajectória da plataforma (cos(2pf t ) >> -1), já quando esta vai a subir (-sin(2p f t ) >0). | ||
Revision as of 17:35, 10 June 2013
Contents
Descrição
Esta experiência consiste num sistema automático de lançamento de dados de seis faces. Para se contarem as pintas, procede-se à aquisição e análise automática da imagem destes dados.
Os valores permitem estudar a lei das probabilidades e elaborar um estudo estatístico de fenómenos aleatórios. Pode-se, também, utilizar as imagens para desenvolver algoritmos próprios, aplicando os mesmos no estudo de várias ferramentas de visão por computador.
Ligações
- Video: [indisponível]
- Laboratório: Básico em e-lab.ist.eu[1]
- Sala de controlo: Aleatório
- Nivel: ***
<swf height="320" width="320">http://www.elab.tecnico.ulisboa.pt/anexos/descricoes-flash/EstatisticaDados.swf</swf>
Aparato Experimental
A experiência consiste num altifalante posicionado na horizontal com uma plataforma no topo do cone de k-line (cartão estruturado com poliuretano), onde se encontram espalhados 14 dados. Na parte superior, a 30 cm da plataforma, está uma câmara de vídeo e um led branco de alto brilho para iluminar a plataforma.
O lançamento dos dados é conseguido através da excitação do altifalante com uma onda sonora, vibrando a plataforma com a mesma frequência da onda.
Esta plataforma tem uma parede que impede os dados de saírem da plataforma e do campo de visão da webcam. Esta parede é bastante alta, para impedir a entrada de luz que não provenha do seu sistema de iluminação.
Com este aparato, obtêm-se imagens como a da figura 2.
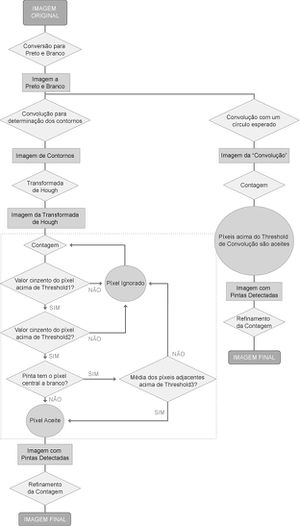
O processamento desta imagem é feito segundo o fluxograma abaixo e o resultado deste processamento leva a uma imagem como a da figura 3.
Manual de Utilização
É possível escolhermos os parâmetros todos da análise de imagem.
- Black&White Threshold: para definir o valor, em escala de cinzento, acima do qual os pixéis ficam a branco.
- Para a Transformada de Hough:
- Threshold1: define o valor acima do qual um pixel da imagem da transformada de Hough é considerado para análise posterior;
- Threshold2: faz a média dos pixéis na vizinhança do pixel que passou o teste anterior e, se essa média for acima deste Threshold2, esse pixel é considerado para análise posterior;
- Threshold3: à partida, qualquer pixel detectado numa zona a branco do dado é desprezado, mas, se esse pixel apresentar uma média (calculada para o teste anterior) superior a este Threshold3, então esse pixel é aproveitado. Isto, porque os dados têm, por vezes, o centro das pintas a branco.
- Convolution Thresold: define o valor acima do qual um pixel da imagem da convolução é considerado para análise posterior;
- Propriedades dos dados:
- Raio da pinta: raio esperado, em pixéis, para a(s) pinta(s) do(s) dado(s) (Nota: Este algoritmo espera que as pintas sejam circulares).
- Largura do dado: distância máxima, em pixéis, entre pintas. Ou seja, para dados de 6 pintas, esta será a distância duma pinta num canto ao outro, na diagonal.
- Número de dados esperado: quantidade de dados esperada. Se for detectada uma quantidade superior e alguns desses não forem detectados como "compatíveis" com dados, então estes serão eliminados (Nota: O algoritmo compara as posições das pintas com conjuntos detectados, com base na proximidade das pintas. Estes conjuntos são comparados com o que se espera obter num dado com a quantidade de pintas que esse conjunto tiver; se essa comparação der positiva, o conjunto fica marcado como "compatível", se não tenta-se fazer trocas e/ou eliminação de pintas até se obter conjuntos "compatíveis" com dados).
Protocolo
O protocolo de execução da experiência é simples porque consiste em excitar, convenientemente, a plataforma para que esta consiga baralhar os dados. De seguida, descreve-se os principais elementos do configurador da sala de controlo para uma melhor compreensão dos mesmos.
Som (lançamento dos dados)
Os dados são lançados (baralhados) pelo movimento oscilante da plataforma onde se encontram. Pode-se seleccionar as frequências inicial e final da onda sonora que vai ser transmitida à plataforma de lançamento dos dados. Esta onda é gerada na altura, ou seja, não há uma colecção de ficheiros de som que já estão gravados com todas as combinações possíveis.
A frequência mínima possível é 20 Hz e a máxima é de 150 Hz.
Abaixo de 20 Hz, não há resposta do altifalante, do amplificador, nem da placa de som que permita a vibração da plataforma. Acima dos 150 Hz, por inércia, a vibração da plataforma tem uma amplitude muito reduzida, logo não é suficiente para comunicar movimento aos dados.
Escolhemos também a duração desta onda sonora, com um mínimo de 1.5 s e um máximo de 10 s. 1.5 s é suficiente para os dados se baralharem um pouco mas para certas frequências perto dos limites, são poucos os que mudam a face virada para cima. 10 s já permite que haja uma desordem dos dados bastante elevada embora desnecessária na maioria dos casos.
Imagem
Escolhemos quantas imagens pretendemos analisar, ao escolher o número de amostras. No mínimo podemos ter uma amostra e, no máximo, vinte.
Uma amostra serve para verificarmos como funciona o motor de detecção, quais os passos que ele segue e quanto tempo demora em cada passo. Com vinte amostras é possível vermos a distribuição que se espera aproximar à “gaussiana” (apesar de tal só acontecer, em teoria, para trinta amostras, pelo menos).
Video
Podemos escolher ver ou não o vídeo do processo de baralhar os dados.
Este vídeo é composto por uma sequência de imagens em formato .jpeg, logo não é um vídeo no verdadeiro sentido da palavra, podendo demorar a transferência de dados de acordo com a velocidade da rede.
Visto que o vídeo exige uma elevada utilização da largura de banda disponível, é aconselhável o seu uso apenas para uma amostra e para ver uma única vez, com intuito lúdico, dado que se torna repetitivo.
Protocolo Avançado
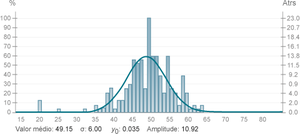
Após a aquisição de suficientes contagens, constrói-se um gráfico do número de ocorrências e faz-se um ajuste à função de distribuição Gaussiana esperada, representada por:
\[ p(x) = y_0 + A e ^{- \frac{(x- \mu)^2}{\sigma ^2}} \]
Como se têm 14 dados, espera-se que o valor mais provável seja 49, o que é comprovado por este ajuste efectuado pela acumulação de valores.
A melhor forma de realizarmos este estudo é articular os resultados de vários utilizadores e verificarmos como melhora o ajuste em função do número crescente de amostras adicionadas.
O valor esperado para o valor médio do lançamento de N dados de seis faces é dado por:
\[ \bar{\mu} = \frac{6N+N}{2} \]
Estudo da frequância ideal para excitar os dados
Suposições:
- O dado que parte do repouso acompanha o movimento ascendente da plataforma;
- O dado apenas se separa da plataforma quando esta começa a descer, ou seja, o dado fica em queda livre, com velocidade inicial vertical nula;
- O choque do dado com a plataforma é inelástico, ou seja, volta a acompanhar a plataforma até à seguinte posição máxima desta.
Assim, partindo do momento em que o dado larga a plataforma, ou seja, quando esta começa a descer, podem-se escrever as seguintes expressões para os movimentos do dado e da plataforma:
Dado: \( y(t) = \frac{A}{2} - \frac{g ^2}{2} \)
Plataforma: \( y'(t) = A cos(2 \pi f t) \)
Nestas expressões: A é a amplitude com que a plataforma vibra; g é a aceleração da gravidade; f é a frequência de vibração da plataforma e t é o tempo desde o momento indicado anteriormente.
Igualando e resolvendo em ordem a t, obtém-se a seguinte equação implítcita:
\[ t = \sqrt{\frac{A- 2 A cos (2 \pi f t)}{g}} \]
Para resolver esta equação, usou-se um método numérico que, essencialmente, tendo um valor de t inicial, avalia a raiz e atribui o valor encontrado à variável t. Volta a repetir este processo até que o valor de t convirja. Obviamente, tem que se ter os valores da amplitude, da frequência e da aceleração da gravidade fixos; usou-se, para a amplitude, 3 mm; para a frequência, usaram-se várias entre 1 e 500 Hz e para a aceleração da graviadade, usou-se 9,81 \(ms^{-2}\).
O valor de t usado para a primeira iterada é de 1/4f, para que o coseno, dentro da raiz, dê zero e a primeira iterada dê um valor real.
Na seguinte tabela estão indicadas as frequências e t para as quais o método convergiu, tal como os cos e sin correspondentes:
| f (Hz) | t (miliseg.) | cos(2p f t ) | - sin(2p f t ) |
|---|---|---|---|
| 14 | 27.91 | -0.7732 | -0.6341 |
| 15 | 29.70 | -0.9418 | -0.3362 |
| 16 | 30.24 | -0.9948 | -0.1017 |
| 17 | 30.25 | -0.9960 | 0.0893 |
| 18 | 29.98 | -0.9692 | 0.2462 |
| 19 | 29.54 | -0.9268 | 0.3756 |
| 20 | 29.01 | -0.8758 | 0.4827 |
| 21 | 28.42 | -0.8206 | 0.5715 |
| 49 | 30.21 | -0.9924 | 0.1227 |
| 50 | 30.26 | -0.9968 | 0.0805 |
| 51 | 30.06 | -0.9781 | 0.2083 |
| 83 | 30.26 | -0.9973 | 0.0736 |
| 116 | 30.27 | -0.9977 | 0.0680 |
| 149 | 30.27 | -0.9980 | 0.0632 |
| 182 | 30.27 | -0.9983 | 0.0591 |
| 215 | 30.27 | -0.9985 | 0.0554 |
| 248 | 30.28 | -0.9986 | 0.0521 |
| 281 | 30.28 | -0.9988 | 0.0491 |
De notar que, regra geral, as trajectórias cruzam-se perto do mínimo da trajectória da plataforma (cos(2pf t ) >> -1), já quando esta vai a subir (-sin(2p f t ) >0).