Dice Statistics
Contents
Description
This experiment consists on a apparatus that automatically shuffle a set of six-sided dice. To count the spots, it acquires and process an image recognition pattern from each side of these dice.
By recording the number of times each side appears, one can to study the law of probabilities and develop a statistical study of random phenomena. We can also use the images to develop special algorithms applied it in the study of several recognition software's.
Experimental Apparatus
In this experiment there is an loudspeaker positioned horizontally with a platform on top of the cone made of k-line (structured light cardboard with polyurethane), where fourteen dice are spread. Above it, at 300mm from the platform is a video camera equiped with a white high brightness LED to illuminate it.
The release (i.e. shuffling) of the dice is achieved trough the exciting of the speaker with a sound wave, which makes the platform to vibrate with the same frequency of the wave.
This platform has a wall that prevents the dice from leaving the platform (and the field of view of the web-cam). The wall is quite high to prevent the entry of light from outside of the lighting system.
With this apparatus, pictures are obtained as we can see in figure 2.
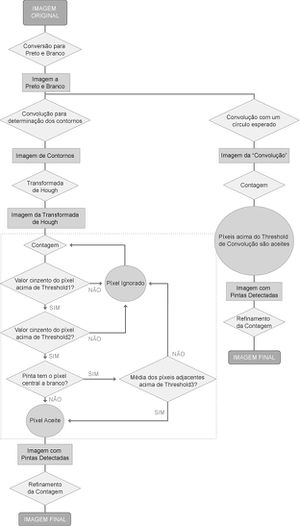
The image processing is made according to the flowchart below and the result of this process leads to an image like the one in figure 3.
Protocol
The execution protocol of the experience is simple because consists in excite, conveniently, the platform so that it can scramble the dice. And then, we describe the main features of the configurator control room for a better understanding thereof.
Dice shuffling
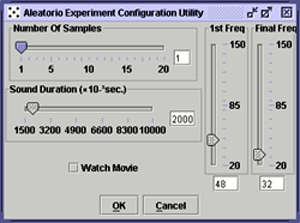
The dice are release (shuffled) by the oscillating movement of the platform where they are. The user can select the starting and ending frequencies of the sound wave that will be transmitted to the platform. This sound wave is synthesized on demand, there are no pre-recorded sound files.
The frequency can be chosen between 20Hz and 150Hz. Bellow 20Hz there is no response from the hardware to vibrate the platform; above 150Hz, the inertia "forces" a low amplitude motion, so the dice don't move.
The user can also choose the duration of the sound wave from 1.5 to 10 seconds. The lower value is enough for shuffle some of the dice at lower frequency but it will ultimately result in a small randomization. The upper limit allows very high randomization and is even unnecessary in some cases.
Pictures
The user chooses how many pictures should be analysed by choosing the number of samples, between 1 and 20.
One sample can be used to check how the recognition software works (what are the steps and how long they take). With 20 samples the results start to show a distributions that evolves towards the Gaussian distribution (even though, in theory, this only happens after 30 samples, minimum).
Video
The user can choose wheather or not to see the video of the shuffling process.
This video is composed of a series of .jpg pictures, which means that it is not an actual video, and the rate of display can change substancially with the connection quality.
Since the video feed has a high demand on the internet connection, the user is advised to use it only once, since it's purpose is mearlly to satisfy cuiriosity.
Advanced Protocol
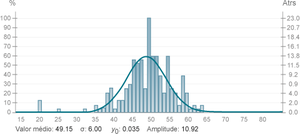
After enough samples, a graph can be constructed with the number of times each number is recorded, as a Gaussian distribution can be fitted:
\[ p(x) = y_0 + A e ^{- \frac{(x- \mu)^2}{\sigma ^2}} \]
Since there are 14 dice, the expected value is 49, which is confirmed by the fitting to the build-up of values.
The best way to cunduct this study is to join the results of several users and see and the fit is improved with increasing number of samples.
The expected value for the average of N 6-sided dice is:
\[ \bar{\mu} = \frac{6N+N}{2} \]