Difference between revisions of "World Pendulum"
| Line 87: | Line 87: | ||
A local apparatus manufacture is an easy task for those interested in their local "<em>g</em>" comparison with the remote experiment . The collection of data through a suitable social network could provide even more data for a complete description of “<em>g's</em> constants” around the globe. | A local apparatus manufacture is an easy task for those interested in their local "<em>g</em>" comparison with the remote experiment . The collection of data through a suitable social network could provide even more data for a complete description of “<em>g's</em> constants” around the globe. | ||
This “world experiment” could be a strong link among various schools for a propitious physics dissemination and dialogue. | This “world experiment” could be a strong link among various schools for a propitious physics dissemination and dialogue. | ||
| − | |||
| − | |||
=Theory involved= | =Theory involved= | ||
Revision as of 20:05, 14 November 2012
Contents
Description
The aim of this world experiment is to provide a constellation of pendulums across several latitudes to investigate the gravitational constant behaviour around the globe. It is expected to have several countries among CPLP contributing to this effort through their own high schools in complement to the e-lab on-line offer.
Sponsors who contributed for this experiment
Experimental apparatus
The pendulum used has been design and constructed by Dr. Jodl team in Germany [1]. Minor changes have been introduced in the IST version. The following data have been used:
|
String length (not counting the sphere) |
2705mm +/- 0.5mm |
|
Sphere mass |
2kg +/- 75g |
|
Sphere radius |
81.5mm +/-0.5mm |
|
String |
Remanium(r) - Stainless steel (Nickel chromium) - 0,4mm |
|
Modulus of elasticity of string |
~200GPa |
|
Oscillation period measurement system |
Micro processor with 7,3728MHz - 30ppm crystal + laser + PIN photodiode |
|
Wire CTE (25-500ºC) (Coefficient of thermal expansion) |
~14 x 10-6 K-1 |
The experiment can be very easily replicated as for local gravity determination it can be human operated without the photo-gate and the microprocessor. The stainless steel can be replace by brass structures.
Local parteners
The pendulum [3] is one of the simplest apparatus with a lot of physics inside. As a matter of fact only the exact measurement of the hanging string and its material quality as to be precise and careful selected to have very accurate measurements. Choosing a heavy mass (e.g. 1-4 kg) the error regarding the period can be made relatively low, allowing an accurate measurement with the use of a simple although precise chronometer.
A local apparatus manufacture is an easy task for those interested in their local "g" comparison with the remote experiment . The collection of data through a suitable social network could provide even more data for a complete description of “g's constants” around the globe. This “world experiment” could be a strong link among various schools for a propitious physics dissemination and dialogue.
Theory involved
The determination of earth gravitational force in different parts of the globe leads to interesting questions about how modelling in physics is so important. Starting from the basic premise that the gravitational accelerating force at sea level is constant, it can be showed very easily that this “constant” slightly changes and has to be corrected mostly due to latitude. So, a very interesting approach to demystify science and some “constants” can be to pursuit the addition of successive stages of approximation to this estimate. The starting point of this undertaking is of course the basic approach to the geophysical model of earth as a simple (i) non-rotating (ii) sphere which gives the very well known approximation of 9.82 m/s2. By symmetry reasons this model leads to a non-dependent latitude dependence on the gravitational acceleration and consequently can be measured in any place on earth disrespect its latitude [1]. But as soon as we progress on the model we will find that a rigorous measurement depends on latitude mainly due to (i) the centrifugal force originating from earth’s rotation and (ii) the non-spherical mass distribution caused by the earth’s poles flattening. These two effects are the most contributing ones being almost of the same amplitude and far more important than (i) altitude, (ii) tides or (iii) sub-sole earth’s density. To conduct a fine-tuning to these evidences, one has to determine the earth’s acceleration in several latitudes across the globe being a difficult task for any student. With this advance in the earth’s acceleration determination, students could easy question the gravitational “constant” and study superior methods for the correct interpretation of earth gravitational force.
A possible way to overcome this difficulty is to have a constellation of experiments across the globe easily reached by the internet.
CPLP as “latitude provider”
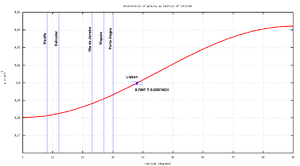
Mother language is one of the nation’s indicators factors and currently is the easier way to define what nations are designate as brother’s (“países irmãos”). Basically only four languages are spread around the globe being the Portuguese one of them. In particular the Portuguese community covers latitudes from ~30S to ~40N, almost a 75º span across the equator, giving an opportunity to operate as a latitude provider for the world pendulum constellation (see Figure).
Effectively to conduct this world experiment we need to consider at least four spaced points in order to have a proper fit. But due to the strong non-linearity of the equation more points are needed to provide a suitable adjustment in particular on the knee close to the earth’s equator. Brazil itself can provide almost four crucial points close to equator (e.g. Recife 8º, Salvador – 12º, Rio de Janeiro – 23º, Porto Alegre – 30º but lacks points with latitude where the characteristic varies more strongly, the almost linear region around 30º to 60º, where Portugal can give two good points, e.g. 37º and 41º. Mozambique can contribute for 27º (Maputo) and S. Tomé e Principe or Brazil are both good choices to cover the equator. Angola could give complementary points for those acquired in Brazil as the sensibility of the measurement is more pronounced close to equator and the poles.
Data fit
Reference [3] gives a very good description of the mathematical model needed to fit the data once established. The main harmonic equation to be fitted can be expressed generally: \[ g_{n}(\varphi) = 9.780 326 772\times[1 + 0.005 302 33 \cdot sin^{2}(\varphi) - 0.000 005 89 \cdot sin^{2}(2\varphi)] \] where \(\varphi\) is the latitude. This formula takes into account the fact that the Earth is an ellipsoid and that there is an additional increase in the acceleration of gravity when one moves nearer to the poles, due to a weaker centrifugal force. Nevertheless the students could derive a non-harmonic, first order approximation taking into account only the centrifugal force. As a second step they could include the two major errors, the centrifugal force and earth’s ellipsoid format.
In the figure it is showed the expected deviation from “earth’s constant acceleration”, the real acceleration for each latitude. We have plotted the point already obtained with this apparatus in Lisbon and the marks over the expected latitudes for future partners. Of course these approximations do not include another important source of deviation from real data to the mathematical model as we do not include the experimental source of error. However those systematic errors could be under the expected precision needed (0,1%) for the former approximation if a careful design of the apparatus is considered. Nevertheless those errors must be discussed in advanced courses and proved their weight when considering the real pendulum.
Bibliography
[1] World pendulum—a distributed remotely controlled laboratory (RCL) to measure the Earth's gravitational acceleration depending on geographical latitude, Grober S, Vetter M, Eckert B and Jodl H J, European Journal of Physics - EUR J PHYS , vol. 28, no. 3, pp. 603-613, 2007
[2] http://rcl-munich.informatik.unibw-muenchen.de/
[3] Physics for scientists and engineers, 5th edition, Hardcourt College Publishers, R.Serway and R. Beichner, 2000
[4] Nelson, Robert; M. G. Olsson (February 1987). "The pendulum - Rich physics from a simple system". American Journal of Physics 54 (2): doi:10.1119/1.14703
[5] Pendulums in the Physics Education Literature: A Bibliography, Gauld, Colin 2004 Science & Education, issue 7, volume 13, 811-832 (http://dx.doi.org/10.1007/s11191-004-9508-7)
[6] The exact equation of motion of a simple pendulum of arbitrary amplitude: a hypergeometric approach, M I Qureshi et al 2010 Eur. J. Phys. 31 1485(http://dx.doi.org/10.1088/0143-0807/31/6/014)
[7] A comprehensive analytical solution of the nonlinear pendulum, Karlheinz Ochs 2011 Eur. J. Phys. 32 479 (http://dx.doi.org/10.1088/0143-0807/32/2/019)