Photovoltaic panel
Contents
Experiment description
Photovoltaic solar energy is a clean, renewable and fast-growing source of energy. Photovoltaic panels use solar radiation to produce electricity, which can be used locally or injected into the electrical grid.
The current experiment intends to study several factors that affect the characteristic, efficiency and power output of a particular photovoltaic panel. To achieve this, a fixed LED panel containing several RGB LEDs was used as the source of radiation for a photovoltaic panel, which can rotate and, consequently, vary the angle it makes with the LED panel. Furthermore, the load resistance connected to the photovoltaic panel can also be varied, enabling the study of how this quantity affects the voltage, currrent and power yielded by the photovoltaic panel.
This simple setup allows the simulation and analysis of the most relevant factors affecting the use of photovoltaic panels in a real environement, contributing to the understanding of the challenges and details related to such use.
Links
- Video: rtsp://elabmc.ist.utl.pt/mag3d.sdp
- Laboratory: Intermediate in elab.tecnico.ulisboa.pt
- Control Room: Mag_3D
- Recording
- Grade: **
Experimental Apparatus
Description
The experimental apparatus used for the present experiment is composed by three main components:
- LED panel
- a fixed panel containing 162 RGB LEDs of model XXXX, organised into a 18 x 9 grid. Each one of this RGB LEDs is internally composed by 3 LEDs (red, green and blue) which can be independently controlled, enabling the selection of any desired color.
- Photovoltaic panel
- a POLY-MONO-XXXX-crystalline photovoltaic panel assembled on top of a rotating axis. This axis is connected to a servo motor which allows the rotation of the panel and, consequently, the variation of the angle between the LED and photovoltaic panels.
- Variable load resistor
- the photovoltaic panel is connected to a variable resistor which acts as the load being powered by the panel. The value of such resistance can also be varied.
The dimensions of the LED and photovoltaic panels can be seen on table XXXX.
| RGB LEDs | 99 \(\times\) 99 |
| Photovoltaic | 99 \(\times\) 99 |
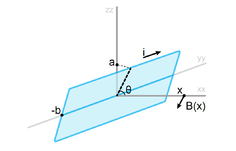
A schematic representation of the experiment is shown in figure XXXX. It is important to note that the placement of the photovoltaic panel at 0º corresponds to having both panels parallel, i.e., the maximum of radiation emitted by the LED panel is reaching the photovoltaic panel. The opposing limit corresponds to the photovoltaic panel at 90º, making both panels perpendicular.
Finally, the user should take into account that the 3 internal LEDs (red, green and blue) composing each one of the RGB LEDs emit with different intensities due to their different wavelengths and productions processes. This way, table XXXX shows the relation between the power (XXXX or intensity? check units!) emitted by the various LEDs' colors.
| Colour | Power (unit!) |
| Red (R) | 999 |
| Green (G) | 999 |
| Blue (B) | 999 |
Configuration
The user can define the following experimental parameters:
- Red (R) intensity
- From 0 to 255, corresponds to the intensity of the red component according to the RGB color model;
- Green (G) intensity
- From 0 to 255, corresponds to the intensity of the green component according to the RGB color model;
- Blue (B) intensity
- From 0 to 255, corresponds to the intensity of the blue component according to the RGB color model;
- Angle
- From -20º to 100º, it is the angle between the photovoltaic and LED panels, as shown by figure XXXX;
- Load resistor
- From 1 to 100, this quantity is proportional to the load resistor connected to the photovoltaic panel;
Moreover, the experiment can be executed in three different modes:
- Angle sweep
- the photovoltaic panel is rotated from -20º up to 100º with steps of 1º, maintaining the selected color and load resistor constant;
- Load resistor sweep
- the value for the load resistor is varied from 1 to 100 with steps of 1, maintaining the selected color and angle constant;
- Load resistor findmax
- for a given selected color and angle, the value of load resistor which maximizes the power extracted from the panel is automatically found through an iterative process;
Results
After launching the experiment, a table is returned with the date/hour of each measurement, the angle between the panels, the value of the load resistor, and the elements measured in each point: the voltage and current on the load resistor, and the total power consumed on this resistor.
Furthermore, the application allows the visualization in real time of the data being collected.
Physics
Semiconductors
Solar cells are based on silicon p-n junctions. Pure silicon is an intrinsic semiconductor with an electrical conductivity of about 2500 \(\Omega \cdot m\), which means it is not a conductor nor an insulator. A pure semiconductor can be doped by adding specific impurity ions, creating extrinsic semiconductors. Taking into account that silicon has 4 valence electrons, impurity dopant ions of less valency will become electron acceptors and impurities of higher valency become electron donors. For the first case, if there are not any free electrons, positively charged states will be produced; these are known as holes and move through the material acting as majority carriers. In the case of electron donors, there will be an excess of free electrons which act as the majority carriers. For doped silicon, typical values of electrical conductivity are around 10 \(\Omega \cdot cm\). \par
P-N junctions
When a p-type material comes into contact with an n-type material, a region of dopant change is created - the p-n junction. When such a junction is created, excess donor electrons from the n-type material move to the acceptor p-type material and the excess holes from the p-type material move to the n-type material, which happens until a steady state is reached. Under this state, the electric field caused by the accumulation of charges of opposite sign on each side of the junction balances the diffusive forces arising from the different concentrations of free electrons and holes. Around the interface between the p and n-type materials, a zone without majority carriers is created. This zone is called depletion zone.
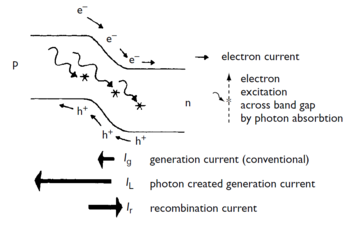
In such a junction, pairs of electrons and holes can be spontaneously generated from bound states, mainly due to thermal excitation. When these carriers are generated in or are able to diffuse to the depletion zone, they are pulled electrostatically down their respective potential gradients, creating a constant generation current, \(I_g\). To maintain the overall balance of current across the depletion zone, there is a reverse recombination current, \(I_r\), that results from the recombination of electrons and holes coming from different sides of the junction. Each electron-hole recombination event corresponds to the transport of one elementary charge across the junction. If the p-n junction is not illuminated and has no external bias, there will be no net current because \(I_r=I_g\). However, if a positive, forward, external bias across the junction, \(V_b\), is applied, the recombination current will be \(I_r = I_g \cdot e^{eV_b/k_B T}\), which will result in a net current in the dark, \(I_D\):
[math] I_D = I_r - I_g = I_g \cdot (e^{eV_b/k_B T}-1) [/math]
This expression is very similar to the characteristic of a diode, with the only difference being that, in a diode, \(I_g\) is replaced by \(I_0\), the saturation current.
Photon absorption at P-N junction
When a p-n junction is exposed to electromagnetic radiation, a process of electron-hole formation causes its absorption. As previously seen, such formation of an electron-hole pair results in the creation of two charge carriers. If this charge carrier creation occurs near a p–n junction, the built-in field across the depletion zone prevents recombination and produces a current, \(I_L\), in an externally connected circuit. This current is much larger than the current arising from the thermal generation of electron-hole pairs already present, which makes the p-n junction behave as a current source. The net current produced is given by:
[math] I = I_D - I_L = I_g \cdot (e^{eV_b/k_B T}-1) - I_L [/math]
Figure XXXX shows the different types of current existing on a illuminated p-n junction.
Experimental studies
...
Bibliography
Links
versão pt!