Difference between revisions of "Photovoltaic panel"
| (9 intermediate revisions by the same user not shown) | |||
| Line 1: | Line 1: | ||
=Experiment description= | =Experiment description= | ||
| − | [[File:Pv panel photo.jpg||thumb|Fig. 1 - Photo of the experimental apparatus. |right|border|300px]] | + | [[File:Pv panel photo.jpg||thumb|Fig. 1 - Photo of the experimental apparatus composed by the tri-color LED panel, the amorphous photovoltaic panel and the controller. |right|border|300px]] |
| − | Photovoltaic solar energy is a clean, renewable and fast-growing source of energy. Photovoltaic panels use solar radiation to produce electricity, which can be used locally or injected into the electrical grid. | + | Photovoltaic solar energy <ref>Handbook of Photovoltaic Science and Engineering, Antonio Luque; Steven Hegedus (editors), 2011, 2 Edition John Wiley & Sons. |
| + | </ref> is a clean, renewable and fast-growing source of energy. Photovoltaic panels use solar radiation to produce electricity, which can be used locally or injected into the electrical grid. | ||
The current experiment intends to study several factors that affect the characteristics, efficiency and power output of a particular photovoltaic panel. To achieve this, a fixed LED panel containing several RGB LEDs was used as the source of radiation for a photovoltaic panel, which can rotate and, consequently, vary the angle it makes with the LED panel. Furthermore, the load resistance connected to the photovoltaic panel can also be varied, enabling the study of how this quantity affects the voltage, current and power yielded by the photovoltaic panel. | The current experiment intends to study several factors that affect the characteristics, efficiency and power output of a particular photovoltaic panel. To achieve this, a fixed LED panel containing several RGB LEDs was used as the source of radiation for a photovoltaic panel, which can rotate and, consequently, vary the angle it makes with the LED panel. Furthermore, the load resistance connected to the photovoltaic panel can also be varied, enabling the study of how this quantity affects the voltage, current and power yielded by the photovoltaic panel. | ||
| Line 12: | Line 13: | ||
<div class="mw-collapsible-content"> | <div class="mw-collapsible-content"> | ||
| − | *Video: | + | *Video: rtsp://elabmc.ist.utl.pt/fotovoltaico.sdp |
| − | *Laboratory: | + | *Laboratory: Basic at [http://elab.tecnico.ulisboa.pt elab] |
| − | *Control | + | *Control room: Photovoltaic |
| − | *[ | + | *[https://www.youtube.com/watch?v=9fRE4WB3mfE Youtube] |
| − | * | + | *Level: * |
</div> | </div> | ||
</div> | </div> | ||
| − | |||
=Experimental Apparatus= | =Experimental Apparatus= | ||
==Description== | ==Description== | ||
| − | [[File:Pv_panel.jpg||thumb|Fig. | + | [[File:MatrizLedAzul.jpg||thumb|Fig. 2 - Detail of the lighting panel composed of a matrix of RGB leds. |right|border|150px]] |
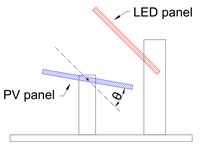
| + | [[File:Pv_panel.jpg||thumb|Fig. 3 - Schematic representation of the experiment. The LED panel is fixed and the photovoltaic panel can rotate around an axis, varying the angle of incidence of the light rays. |right|border|200px]] | ||
The experimental apparatus used for the present experiment is composed of three main components: | The experimental apparatus used for the present experiment is composed of three main components: | ||
| Line 80: | Line 81: | ||
;Load resistor: | ;Load resistor: | ||
:From 1 to 100, this quantity is proportional to the load resistor connected to the photovoltaic panel; | :From 1 to 100, this quantity is proportional to the load resistor connected to the photovoltaic panel; | ||
| + | |||
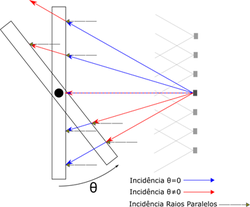
| + | [[File:Fotovoiltaico raios.png||thumb|Fig. 4 - Scheme of the light rays incidence: this case differs from the sun rays. Its geometry implies that they are not parallel. The various possible angles of incidence of a particular led are evidenced in two different situations of positioning the panel.|right|border|250px]] | ||
| Line 116: | Line 119: | ||
<math> I = I_D - I_L = I_g \cdot (e^{eV_b/k_B T}-1) - I_L </math> | <math> I = I_D - I_L = I_g \cdot (e^{eV_b/k_B T}-1) - I_L </math> | ||
| − | Figure | + | Figure 5 shows the different types of current existing on an illuminated p-n junction. |
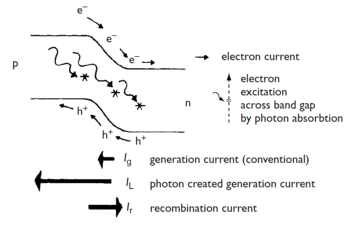
| − | [[File:Photon_absor.PNG||thumb|Fig. | + | [[File:Photon_absor.PNG||thumb|Fig. 5 - Different currents existing on an illuminated p-n junction. |center|350px]] |
=Experimental studies= | =Experimental studies= | ||
| − | ... | + | The execution of the three experimental protocols described allows the collection of data for the characterization of the photovoltaic panel’s response. Some study protocols are listed below. |
| + | |||
| + | ===Angle Sweep=== | ||
| + | |||
| + | By changing the angle and keeping constant the lighting conditions, it is possible to verify how the power produced by the panel varies depending on the lighting angle. It is important to highlight that, in the experiment, the rays do not strike in parallel as in the solar radiation, so it is possible to define an effective angle that involves a slower tempo than the real angle. | ||
| + | |||
| + | To determine the effective value of radiation, when adjusting a first sinusoidal model (using, for example, the cosine of the angle), the multiplicative factor of the angle must be discovered by the appropriate adjustment of the function. It is suggested to use a function <math> P_{ger} = A\cos(gain\cdot \theta)</math>, where the gain is of the order of unit but always greater. Looking at figure 4, with the panel at 90º, it still receives light. If the rays were parallel, it would be completely obscured. | ||
| + | |||
| + | ===Load Resistance Sweep=== | ||
| + | |||
| + | The maximum transfer of power between a generator (the panel, in this case) and its load (resistance that dissipates the produced energy) is obtained when there is a so-called impedance adaptation, that is, when the internal resistance of the generator is equal to the load. | ||
| + | |||
| + | In this protocol, it is suggested to sweep the electrical resistance of the load. In this way, it will be possible to obtain the impedance that best suits depending on (i) the intensity of the light and (ii) the angle selected. | ||
| + | |||
| + | Initially, the generated power increases with the load resistance, since the panel keeps the current at its terminals approximately constant, but the generated voltage increases. However, after a certain load value, the panel reaches its maximum generated current. An increase of the load results in a decrease of the voltage at the panel terminals and, consequently, a decrease of the power generated by it. This result is very important for the operation of a photovoltaic panel. It is verified that in order to obtain the maximum power, that is, to operate the panel at the most efficient point, it is necessary to adapt the load resistance to the impedance of the panel that relates directly to the power of the incident light. | ||
| + | |||
| + | This impedance can be easily calculated using the Ohm’s Law since the voltage and current generated by the panel are accessible. | ||
| + | |||
| + | ===Maximum power search=== | ||
| + | By executing the protocol for searching the load resistance that generates maximum power, it is possible to directly obtain the value that maximizes the power for the configured angle and luminosity, calculating, as explained in the previous section, the value of the load resistance of the penultimate sampled point. | ||
| + | |||
| + | Using the measured values, it turns out that the maximum occurs for ~ 80%; the influence of the radiation color (wavelength) can be studied and the optimal load resistance can be determined. The load resistance value that maximizes the generated power could also be obtained by directly reading the graph produced in the previous protocol. | ||
| + | ===Other studies=== | ||
| + | In addition to the previous suggestions, focused on the 3 experimental protocols, the experiment also allows studying (i) the validity of the parallel ray approximation that is frequently used, developing a more complete model; (ii) the influence of dispersed light on the experience and on the obtained results; (iii) the functioning of solar charge controllers (MPPT), proposing other algorithms and lastly, (iv) the influence of wavelength on the photovoltaic cells efficiency. | ||
=Bibliography= | =Bibliography= | ||
| Line 131: | Line 157: | ||
=Links= | =Links= | ||
| − | *[[ Painel fotovoltaico | Portuguese Version (Versão em Português)]] | + | *[[Painel fotovoltaico | Portuguese Version (Versão em Português)]] |
Latest revision as of 16:28, 17 May 2021
Contents
Experiment description
Photovoltaic solar energy [1] is a clean, renewable and fast-growing source of energy. Photovoltaic panels use solar radiation to produce electricity, which can be used locally or injected into the electrical grid.
The current experiment intends to study several factors that affect the characteristics, efficiency and power output of a particular photovoltaic panel. To achieve this, a fixed LED panel containing several RGB LEDs was used as the source of radiation for a photovoltaic panel, which can rotate and, consequently, vary the angle it makes with the LED panel. Furthermore, the load resistance connected to the photovoltaic panel can also be varied, enabling the study of how this quantity affects the voltage, current and power yielded by the photovoltaic panel.
This simple setup allows the simulation and analysis of the most relevant factors affecting the use of photovoltaic panels in a real environment, contributing to the understanding of the challenges and details related to such use.
Links
Experimental Apparatus
Description
The experimental apparatus used for the present experiment is composed of three main components:
- LED panel
- a fixed panel containing 162 RGB LEDs of model SMD5050, organised into an 18 x 9 grid. Each one of these RGB LEDs is internally composed of 3 LEDs (red, green and blue) which can be independently controlled, enabling the selection of any desired colour.
- Photovoltaic panel
- a photovoltaic panel assembled on top of a rotating axis. This axis is connected to a servo motor which allows the rotation of the panel and, consequently, the variation of the angle between the LED and photovoltaic panels.
- Variable load resistor
- the photovoltaic panel is connected to a variable resistor which acts as the load being powered by the panel. The value of such resistance can also be varied.
The dimensions of the LED and photovoltaic panels can be seen in the following table.
| RGB LEDs | 14.5 \(\times\) 9 |
| Photovoltaic | 15 \(\times\) 10 |
A schematic representation of the experiment is shown in figure 2. It is important to note that the placement of the photovoltaic panel at 0º corresponds to having both panels parallel, i.e., the maximum of radiation emitted by the LED panel is reaching the photovoltaic panel. The opposing limit corresponds to the photovoltaic panel at 90º, making both panels perpendicular.
Finally, the user should take into account that the 3 internal LEDs (red, green and blue) composing each one of the RGB LEDs emit with different intensities due to their different wavelengths and productions processes. This way, the table below shows the relation between the luminous flux (intensity of visible radiation) emitted by the various LEDs' colours.
| Colour | Luminous flux (lux) |
| Red (R) | 1080 |
| Green (G) | 5780 |
| Blue (B) | 7320 |
Configuration
The user can define the following experimental parameters:
- Red (R) intensity
- From 0 to 255, corresponds to the intensity of the red component according to the RGB colour model;
- Green (G) intensity
- From 0 to 255, corresponds to the intensity of the green component according to the RGB colour model;
- Blue (B) intensity
- From 0 to 255, corresponds to the intensity of the blue component according to the RGB colour model;
- Angle
- From -20º to 100º, it is the angle between the photovoltaic and LED panels, as shown by figure 2;
- Load resistor
- From 1 to 100, this quantity is proportional to the load resistor connected to the photovoltaic panel;
Moreover, the experiment can be executed in three different modes:
- Angle sweep
- the photovoltaic panel is rotated from -20º up to 100º with steps of 1º, maintaining the selected colour and load resistor constant;
- Load resistor sweep
- the value for the load resistor is varied from 1 to 100 with steps of 1, maintaining the selected colour and angle constant;
- Load resistor findmax
- for a given selected colour and angle, the value of load resistor which maximizes the power extracted from the panel is automatically found through an iterative process;
Results
After launching the experiment, a table is returned with the date/hour of each measurement, the angle between the panels, the value of the load resistor, and the elements measured in each point: the voltage and current on the load resistor, and the total power consumed on this resistor.
Furthermore, the application allows the visualization in real-time of the data being collected.
Physics
Semiconductors
Photovoltaic panels are based on silicon p-n junctions. Pure silicon is an intrinsic semiconductor with an electrical conductivity of about 2500 \(\Omega \cdot m\), which means it is not a conductor nor an insulator. A pure semiconductor can be doped by adding specific impurity ions, creating extrinsic semiconductors. Taking into account that silicon has 4 valence electrons, impurity dopant ions of less valency will become electron acceptors and impurities of higher valency become electron donors. For the first case, if there are not any free electrons, positively charged states will be produced; these are known as holes and move through the material acting as majority carriers. In the case of electron donors, there will be an excess of free electrons which act as the majority carriers. For doped silicon, typical values of electrical conductivity are around 10 \(\Omega \cdot cm\).
P-N junctions
When a p-type material comes into contact with an n-type material, a region of dopant change is created - the p-n junction. When such a junction is created, excess donor electrons from the n-type material move to the acceptor p-type material and the excess holes from the p-type material move to the n-type material, which happens until a steady-state is reached. Under this state, the electric field caused by the accumulation of charges of opposite sign on each side of the junction balances the diffusive forces arising from the different concentrations of free electrons and holes. Around the interface between the p and n-type materials, a zone without majority carriers is created. This zone is called the depletion zone.
In such a junction, pairs of electrons and holes can be spontaneously generated from bound states, mainly due to thermal excitation. When these carriers are generated in or are able to diffuse to the depletion zone, they are pulled electrostatically down their respective potential gradients, creating a constant generation current, \(I_g\). To maintain the overall balance of current across the depletion zone, there is a reverse recombination current, \(I_r\), that results from the recombination of electrons and holes coming from different sides of the junction. Each electron-hole recombination event corresponds to the transport of one elementary charge across the junction. If the p-n junction is not illuminated and has no external bias, there will be no net current because \(I_r=I_g\). However, if a positive, forward, external bias across the junction, \(V_b\), is applied, the recombination current will be \(I_r = I_g \cdot e^{eV_b/k_B T}\), which will result in a net current in the dark, \(I_D\):
[math] I_D = I_r - I_g = I_g \cdot (e^{eV_b/k_B T}-1) [/math]
This expression is very similar to the characteristic of a diode, with the only difference being that, in a diode, \(I_g\) is replaced by \(I_0\), the saturation current.
Photon absorption at P-N junction
When a p-n junction is exposed to electromagnetic radiation, a process of electron-hole formation causes its absorption. As previously seen, such formation of an electron-hole pair results in the creation of two charge carriers. If this charge carrier creation occurs near a p–n junction, the built-in field across the depletion zone prevents recombination and produces a current, \(I_L\), in an externally connected circuit. This current is much larger than the current arising from the thermal generation of electron-hole pairs already present, which makes the p-n junction behave as a current source. The net current produced is given by:
[math] I = I_D - I_L = I_g \cdot (e^{eV_b/k_B T}-1) - I_L [/math]
Figure 5 shows the different types of current existing on an illuminated p-n junction.
Experimental studies
The execution of the three experimental protocols described allows the collection of data for the characterization of the photovoltaic panel’s response. Some study protocols are listed below.
Angle Sweep
By changing the angle and keeping constant the lighting conditions, it is possible to verify how the power produced by the panel varies depending on the lighting angle. It is important to highlight that, in the experiment, the rays do not strike in parallel as in the solar radiation, so it is possible to define an effective angle that involves a slower tempo than the real angle.
To determine the effective value of radiation, when adjusting a first sinusoidal model (using, for example, the cosine of the angle), the multiplicative factor of the angle must be discovered by the appropriate adjustment of the function. It is suggested to use a function [math] P_{ger} = A\cos(gain\cdot \theta)[/math], where the gain is of the order of unit but always greater. Looking at figure 4, with the panel at 90º, it still receives light. If the rays were parallel, it would be completely obscured.
Load Resistance Sweep
The maximum transfer of power between a generator (the panel, in this case) and its load (resistance that dissipates the produced energy) is obtained when there is a so-called impedance adaptation, that is, when the internal resistance of the generator is equal to the load.
In this protocol, it is suggested to sweep the electrical resistance of the load. In this way, it will be possible to obtain the impedance that best suits depending on (i) the intensity of the light and (ii) the angle selected.
Initially, the generated power increases with the load resistance, since the panel keeps the current at its terminals approximately constant, but the generated voltage increases. However, after a certain load value, the panel reaches its maximum generated current. An increase of the load results in a decrease of the voltage at the panel terminals and, consequently, a decrease of the power generated by it. This result is very important for the operation of a photovoltaic panel. It is verified that in order to obtain the maximum power, that is, to operate the panel at the most efficient point, it is necessary to adapt the load resistance to the impedance of the panel that relates directly to the power of the incident light.
This impedance can be easily calculated using the Ohm’s Law since the voltage and current generated by the panel are accessible.
Maximum power search
By executing the protocol for searching the load resistance that generates maximum power, it is possible to directly obtain the value that maximizes the power for the configured angle and luminosity, calculating, as explained in the previous section, the value of the load resistance of the penultimate sampled point.
Using the measured values, it turns out that the maximum occurs for ~ 80%; the influence of the radiation color (wavelength) can be studied and the optimal load resistance can be determined. The load resistance value that maximizes the generated power could also be obtained by directly reading the graph produced in the previous protocol.
Other studies
In addition to the previous suggestions, focused on the 3 experimental protocols, the experiment also allows studying (i) the validity of the parallel ray approximation that is frequently used, developing a more complete model; (ii) the influence of dispersed light on the experience and on the obtained results; (iii) the functioning of solar charge controllers (MPPT), proposing other algorithms and lastly, (iv) the influence of wavelength on the photovoltaic cells efficiency.
Bibliography
- ↑ Handbook of Photovoltaic Science and Engineering, Antonio Luque; Steven Hegedus (editors), 2011, 2 Edition John Wiley & Sons.