Difference between revisions of "Dielectric effect in a Cilindric Capacitor"
m (Agora mudei de PVC para Polystyrene) |
|||
| Line 2: | Line 2: | ||
[[File:condensador-fotografia.png|thumb|Figure 1: Photo of the experimental setup]] | [[File:condensador-fotografia.png|thumb|Figure 1: Photo of the experimental setup]] | ||
| − | This experiment | + | This purpose of this experiment is the determination of the capacity of a variable coax cylindrical capacitor. It has two sections, a first with a Polystyrene dielectric, and a second with air, allowing the determination of the relative dielectric constant of Polystyrene. |
| Line 21: | Line 21: | ||
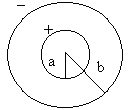
[[File:condensador-seccao.png|thumb|Figure 2: Sectioned schematic of the capacitor, where a=12mm and b=16mm]] | [[File:condensador-seccao.png|thumb|Figure 2: Sectioned schematic of the capacitor, where a=12mm and b=16mm]] | ||
| − | The capacitor is made | + | The capacitor is made of a copper tube with an outer diameter of 12mm and 200mm long (inner plate), having been outfitted with a Polystyrene dielectric to a certain length. This is enclosed in a second copper tube with an inner diameter of 16mm (outer plate), that moves along the first, thus acting as the plates of a variable capacitor. This way, the area of the capacitor corresponds only to the parts where the two cylinders overlap. |
| − | Note that, because of set-up constraints, there is a "minimum" capacitor of 26mm. In other words, x=0 actually corresponds to a cylindrical capacitor | + | Note that, because of set-up constraints, there is a "minimum" capacitor of 26mm. In other words, x=0 actually corresponds to a 26mm long cylindrical capacitor and Polystyrene dielectric. |
| Line 29: | Line 29: | ||
==Determination of the relative dielectric constant== | ==Determination of the relative dielectric constant== | ||
| − | Take two sets of experimental data, one covering the Polystyrene area and the other covering air. The end-points of the sweep should be chosen in a way that allows a precise determination of the slope of the graphical representation. This slope will give the relation between the capacity and the length of the capacitor (each set referring to its corresponding dielectric). The ratio between the two slopes will give the relative dielectric constant | + | Take two sets of experimental data, one covering the Polystyrene area and the other covering air. The end-points of the sweep should be chosen in a way that allows a precise determination of the slope of the graphical representation. This slope will give the relation between the capacity and the length of the capacitor (each set referring to its corresponding dielectric). The ratio between the two slopes will give the relative dielectric constant of Polystyrene. |
| Line 41: | Line 41: | ||
\] | \] | ||
| − | By doing a linear regression with the data from the section of the capacitor without the dielectric (which means the air acts as the dielectric) it is possible to accurately determine the value of the capacity. From this, reversing the formula, the air | + | By doing a linear regression with the data from the section of the capacitor without the dielectric (which means the air acts as the dielectric) it is possible to accurately determine the value of the capacity. From this, reversing the formula, the permittivity of the air can be found (close to vacuum, i.e. \( \epsilon _0 \)). |
Revision as of 23:50, 24 October 2013
Contents
Description of the Experiment
This purpose of this experiment is the determination of the capacity of a variable coax cylindrical capacitor. It has two sections, a first with a Polystyrene dielectric, and a second with air, allowing the determination of the relative dielectric constant of Polystyrene.
Ligações
- Video: rtsp://elabmc.ist.utl.pt/condensador.sdp
- Laboratory: Advanced in e-lab.ist.eu[1]
- Control room: Condensador Cilíndrico
- Level: ****
Experimental Apparatus
The capacitor is made of a copper tube with an outer diameter of 12mm and 200mm long (inner plate), having been outfitted with a Polystyrene dielectric to a certain length. This is enclosed in a second copper tube with an inner diameter of 16mm (outer plate), that moves along the first, thus acting as the plates of a variable capacitor. This way, the area of the capacitor corresponds only to the parts where the two cylinders overlap.
Note that, because of set-up constraints, there is a "minimum" capacitor of 26mm. In other words, x=0 actually corresponds to a 26mm long cylindrical capacitor and Polystyrene dielectric.
Protocol
Determination of the relative dielectric constant
Take two sets of experimental data, one covering the Polystyrene area and the other covering air. The end-points of the sweep should be chosen in a way that allows a precise determination of the slope of the graphical representation. This slope will give the relation between the capacity and the length of the capacitor (each set referring to its corresponding dielectric). The ratio between the two slopes will give the relative dielectric constant of Polystyrene.
Advanced Protocol
Determination of the dielectric constant of air
Considering Gauss's law, it is possible to determine the capacity of the cylindrical capacitor, using the formula:
\[ C = \frac{ 2 \pi \epsilon _0 }{ ln(\frac{b}{a}) } L \]
By doing a linear regression with the data from the section of the capacitor without the dielectric (which means the air acts as the dielectric) it is possible to accurately determine the value of the capacity. From this, reversing the formula, the permittivity of the air can be found (close to vacuum, i.e. \( \epsilon _0 \)).