Determination of Planck's Constant
Contents
Description of the Experiment
The purpose of this experiment is to study the photoelectric effect and calculate Planck's constant using 5 different coloured leds and a photoelectric cell.
Experimental Apparatus
The photoelectric cell is from the PASCO AP-9368 apparatus. It works like a capacitor where one of the plates emits photoelectrons when excited by light. The potential between the plates of the photocell will increase with the emitted photoelectron accumulation. After reaching a certain voltage, the stopping potential will be greater than the photoelectron's kinetic energy, and these will not have enough energy to reach the second plate. This voltage will depend on the wavelength of the incident light (photon energy).
After each experiment the photocell is connected to ground to discharge it.
The leds have different efficiency, leading to different intensities for a chosen brightness. Therefore, the charging time will be different between colors.
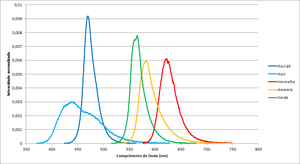
The graph in figure 1 shows each led's spectrum, table 1 having more details.
Please note that the wavelength for each led depends on the junction's temperature, and this will depend not only on room temperature, but also on the current passing through the junction. This effect (red shift) is more noticeable in warm-coloured led (green-red) than blue, so the calculation of Planck's constant will suffer a shift.
| Color | Frequency (THz) | Wavelegth (nm) | Espectros dos leds |
|---|---|---|---|
| Blue.ab | 638.7 | 469.70 | File:Espectro Azul.ab.txt |
| Blue | 684.6 | 438.20 | File:Espectro Azul.txt |
| Red | 482.2 | 622.21 | File:Espectro Vermelho.txt |
| Yellow | 514.4 | 583.16 | File:Example.txt |
| Green | 530.8 | 565.22 | File:Espectro Verde.txt |
Protocol
The number of photoelectrons emitted will increase with the intensity of light (corpuscular behaviour of light).
- Choose a led to light upon the photocell
- Measure the stopping potential. Note the time necessary to reach the maximum potential.
- Repeat step 2 for different intensities.
| Color #1 __________(name) | Intensity (%) | Stop Potential (V) | Time (s) |
|---|---|---|---|
| 100 | |||
| 80 | |||
| 60 | |||
| 40 | |||
| 20 |
The photoelectron's kinetic energy depends only on the frequency of the incident light. If the frequency of light increases, the energy will increase.
- Obtain the stop potentials for different colour leds.
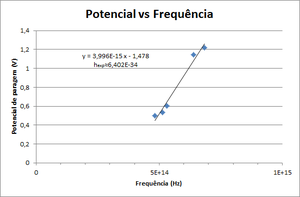
- Draw a graphic of Stop Potential vs Frequency. Fit it to \( V = \frac{h}{e} \nu - \frac{W_0}{e} \) and obtain Planck's constant.
| Colour (name) | Frequency (THz) | Stop Potential (V) |
|---|---|---|
Advanced Protocol
- Study the photocell's charging process for different intensities.
- Find the expected value for wavelength using the led spectra.
- Use those values for a new graphical fitting and compare the results.
- Redo the voltage vs. frequency graph, this time with error bars.
Note: This setup uses a 12bit ADC from 0V to 5V.
Theoretical Principles
Photoelectric effect
The photoelectric effect happens when a metal surface is illuminated by a light with a given frequency, causing electrons to be freed. When a photon with energy \( E \) collides with a metal, it transfers it's energy to an electron in the crystal structure. The emission of electrons is deeply connected to the frequency of the light shone upon the surface. For each metal there is a critical frequency, \( \nu _0 \). If incident radiation has frequency bellow \( \nu _0 \), then there are no emitted electrons. If the former is above the latter, then the kinetic energy of the emitted electrons is proportional to the energy of the photons. The light's intensity changes only the number of emitted photoelectrons, not it's energy (this goes against what is expected in the classical theory of radiation).
Einstein proposed the following explanation: light is made of photons with a given energy, proportional to frequency (\( \nu \)):
\[ E = h \nu \]
Where \( h \) is Planck's constant. The photoelectric effect is, essentially, a collision between a photon (light) and an electron (in the metal) where the former gives all it's energy to the latter. Since the electron's energy is higher when in vacuum (as opposed when it's bound in the metal's crystal structure), the electron is only freed if the photon's energy is higher than the difference between the electron's energy in vacuum and in the metal (figure 1). Thus, the electron leaves the metal with energy equal to the photon's energy minus the amount "spent" when the electron leaves the metal:
\[ E = h \nu - e \phi \]
where \( e \) is the electron charge and \( \phi \) is the diference in workfunction. As the light's frequency decreases, the photons have less energy. Bellow a certain critical frequency \( \nu _0 \), no more photoelectrons are emited. In this case, \( E_{max} = 0 \) and we can write:
\[ h \nu _0 = e \phi \quad or \quad \nu _0 = \frac{e}{h} \phi \]
In This Setup
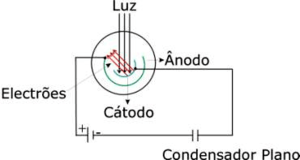
A photoelectric cell is a device where light shines upon a metalic surface (cathode) and exites electrons that will be collected by a concentric metalic surface (anode) like what's shown in the figure on the right (it is basically a semi-cilindric capacitor with very low capacity). If we connect the cathode and anode through an external circuit we can measure the current created by the photoelectrons. In a more generic sense, the electron's maximum kinetic energy is determined by applying a stopping potencial between the cathode and the anode to prevent electrons from reaching the former. This way, when current no longer flows, we will know the the value of the current.
We begin by applying a voltage to the vell (approximatlly 9V, because the capacitor is discharged before starting the experiment by short-circuiting the terminals). With the cell in series with the capacitor, the latter will charge as electrons are generated in the former. This creates an electric current through the cell. As the capacitor charges, the voltage between it's terminals increases, diminuishing the volltage between the cell's terminals (because \( V_{bat} = V_{Cap} + V_{cell} = constant \)). When the cell's voltage reaches \( V_c = \frac{h \nu - e \phi}{e} \), current no longer flows and the capacitor maintains a constant voltage.
Knowing two or more voltage values for certain frequencies the user can do a linear regression and determine both \( \phi \) and Planck's constant. In the following graphic we can see the relation between the stopping potencial V and the light's frequency for a given metal. This function is a linear function with slope = \( \frac{h}{\epsilon} \) and y-intercept = \( \phi \).
Historical Elements
In 1921, Albert Einstein won the Nobel Physics Prize for his work on the photoelectric effect.