Difference between revisions of "Determination of Planck's Constant"
| Line 1: | Line 1: | ||
=Descrição da Experiência= | =Descrição da Experiência= | ||
O objectivo desta experiência é o estudo do efeito fotoeléctrico e a determinação da constante de Planck, usando 5 leds de cores diferentes e intensidade regulável a incidir sobre uma célula fotoeléctrica. | O objectivo desta experiência é o estudo do efeito fotoeléctrico e a determinação da constante de Planck, usando 5 leds de cores diferentes e intensidade regulável a incidir sobre uma célula fotoeléctrica. | ||
| + | |||
=Aparato Experimental= | =Aparato Experimental= | ||
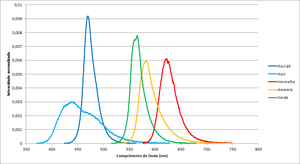
[[File:Espectro_dos_leds.png|thumb|alt=Espectro dos Leds|Figura 1: Espectro dos leds.]] | [[File:Espectro_dos_leds.png|thumb|alt=Espectro dos Leds|Figura 1: Espectro dos leds.]] | ||
| Line 35: | Line 36: | ||
|565.22 | |565.22 | ||
|} | |} | ||
| + | |||
| + | =Protocolo= | ||
| + | Segundo o efeito fotoeléctrico, o numero de fotoelectrões emitidos por unidade de tempo duplica quando a intesidade da luz duplica. (comportamento corpuscular da luz) | ||
| + | |||
| + | #Escolher a cor a incidir sobre a fotocélula. | ||
| + | #Tome nota da tensão de paragem e determine o tempo necessário para atingir a tensão máxima. | ||
| + | #Repita passo 2 para diferentes intensidades. | ||
| + | |||
| + | {| border="1" style="text-align: center;" | ||
| + | |+ Exemplo de uma tabela | ||
| + | |- | ||
| + | !Cor #1 __________(nome) | ||
| + | !Transmissão (%) | ||
| + | !Potencial paragem (V) | ||
| + | !Tempo de carga (s) | ||
| + | |- | ||
| + | | | ||
| + | |100 | ||
| + | | | ||
| + | | | ||
| + | |- | ||
| + | | | ||
| + | |80 | ||
| + | | | ||
| + | | | ||
| + | |- | ||
| + | | | ||
| + | |60 | ||
| + | | | ||
| + | | | ||
| + | |- | ||
| + | | | ||
| + | |40 | ||
| + | | | ||
| + | | | ||
| + | |- | ||
| + | | | ||
| + | |20 | ||
| + | | | ||
| + | | | ||
| + | |} | ||
| + | |||
| + | |||
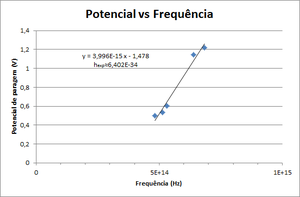
| + | [[File:Constante de Planck.png|thumb|alt=Constante de Planck|Figura 2: Tensão vs. Pico de frequência da luz]] | ||
| + | |||
| + | A energia cinética dos fotoelectrões depende apenas da frequência da luz. Quanto maior for a frequência da luz, maior é a energia. | ||
| + | |||
| + | #Obtenha as tensões de paragem para diferentes cores. | ||
| + | #Fazer um ajuste linear ao gráfico Tensão vs. Frequência e obtenha a constante de Planck. | ||
| + | |||
| + | |||
| + | {| border="1" style="text-align: center;" | ||
| + | |+ Exemplo de uma tabela | ||
| + | |- | ||
| + | !Cor (nome) | ||
| + | !Frequência (Hz) | ||
| + | !Potencial paragem (V) | ||
| + | |- | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | |- | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | |- | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | |- | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | |- | ||
| + | | | ||
| + | | | ||
| + | | | ||
| + | |} | ||
| + | |||
| + | =Protocolo Avançado= | ||
| + | |||
| + | #Calcule a constante de tempo da montagem. | ||
| + | #Encontre os valores esperados do comprimento de onda apartir dos espectros dos leds. | ||
| + | #Refaça o gráfico tensão vs frequência com barras de erro. | ||
| + | |||
| + | Nota: Utilizou-se um ADC 12bit no intervalo de 0V a 5V. | ||
| + | |||
| + | =Princípios Teóricos= | ||
| + | |||
| + | ==Efeito Fotoeléctrico== | ||
| + | O efeito foto-eléctrico consiste na emissão de electrões da superfície de um metal quando este é iluminado por luz de uma dada frequência (\( \nu \)). Um fotão de energia \( E = h \nu \) ao incidir no metal transfere a sua energia a um electrão pertencente a um dos átomos na rede cristalina do metal. A emissão de electrões do metal é muito dependente da frequência da luz incidente. Para cada metal, existe uma frequência critica, \( \nu _0 \), tal que para luz incidente com frequência inferior não há foto-electrões arrancados. Por outro lado, para frequências superiores, a energia dos foto-electrões emitidos aumenta linearmente com a energia dos fotões incidentes. A intensidade da luz incidente afecta somente o número de foto-electrões emitidos, mas não a sua energia, contrariamente ao que seria de esperar na teoria clássica da radiação. | ||
| + | Einstein propôs a seguinte explicação para o fenómeno: a luz é transportada por fotões com uma dada energia E associada à frequência da luz \( \nu \): | ||
| + | |||
| + | \[ | ||
| + | E = h \times \nu | ||
| + | \] | ||
| + | |||
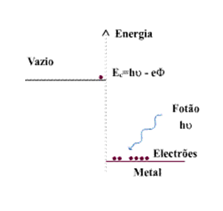
| + | em que ''h'' é a constante de Planck. O efeito foto-eléctrico deve-se a uma colisão do fotão com o electrão, em que aquele transmite a este toda a sua energia. Tendo em conta que a energia de um electrão no vazio e dentro do metal é diferente (mais elevada no vazio), só se verifica efeito foto-eléctrico se a energia transmitida pelo fotão for superior à diferença entre estas duas energias (ver Fig. 1). Assim, a energia com que o electrão abandona o metal é igual à energia do fotão menos a energia "gasta" para o electrão abandonar o metal: | ||
| + | |||
| + | \[ | ||
| + | E = h \times \nu - e \times \phi, | ||
| + | \] | ||
| + | |||
| + | em que ''e'' é a carga do electrão e \( \phi \) é a diferença de ''workfunction''. | ||
| + | Tal como foi anteriormente enunciado, à medida que a frequência da luz incidente decresce, os fotões têm menos energia, e a partir de uma frequência critica \( \nu _0 \) não são emitidos mais foto-electrões. Neste caso, \( E _{max} = 0 \) e da Eq. l tiramos | ||
| + | |||
| + | \[ | ||
| + | h \nu _0 = e \phi \quad ou \quad \nu _0 = \frac{e}{h} \phi | ||
| + | \] | ||
| + | |||
| + | [[File:Plank-teo1.png|thumb]] | ||
| + | |||
| + | |||
| + | ==Efeito Fotoeléctrico== | ||
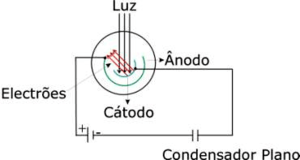
| + | Uma célula foto-eléctrica é um dispositivo onde a luz incidente sobre uma superfície metálica (cátodo) excita electrões que vão ser colectados numa superfície metálica concêntrica (ânodo), tal como exemplificado na figura, e que na prática é um condensador semi-cilíndrico de capacidade muito baixa. Ligando o ânodo e o cátodo por um circuito externo, podemos medir a corrente produzida pelos foto-electrões. No caso mais genérico, a energia cinética máxima dos foto-electrões emitidos é determinada aplicando um potencial de paragem, Vc entre o ânodo e o cátodo de modo a impedir que os foto-electrões emitidos pelo cátodo atinjam o ânodo. Deste modo, deixa de fluir corrente no circuito. | ||
| + | |||
| + | [[File:Plank-celula1.png|thumb]] | ||
| + | |||
| + | A célula inicialmente tem aplicada a tensão da fonte, aproximadamente 9V uma vez que o condensador é descarregado no início da experiência (é efectuado um curto-circuito aos seus terminais). Como a célula está em série com o condensador, este vai carregando à medida que são gerados foto-electrões, criando uma corrente eléctrica no circuito que atravessa a célula. À medida que o condensador carrega, aumenta a diferença de potencial aos seus terminais, o que obriga a diminuir a tensão aos terminais da célula (note que \( V_{bat} = V_{Cond} + V_{célula} = constante \)). Quando a diferença de potencial nas placas da célula for igual a \( V_c = \frac{h \times \nu - e \times \phi}{e} \), deixa de fluir corrente no circuito e o condensador passa a ter uma tensão constante aos seus terminais. | ||
| + | |||
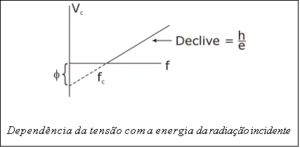
| + | Conhecendo dois ou mais valores dessa tensão para determinadas frequências [1] pode-se efectuar uma regressão linear e determinar não só \( \phi \) mas também a constante de Planck. No gráfico seguinte esquematizamos a dependência da tensão de paragem V em função da frequência da luz incidente para um dado metal. A função em causa corresponde a uma recta de declive \( \frac{h}{e} \) e coeficiente na origem \( \phi \). | ||
| + | |||
| + | [[File:Plank-celula2.png|thumb]] | ||
| + | |||
| + | |||
| + | =Elementos Históricos= | ||
| + | Em 1921 foi atribuído a Albert Einstein o Prémio Nobel da Física pelas suas descobertas no efeito fotoeléctrico. | ||
Revision as of 18:26, 29 September 2012
Contents
Descrição da Experiência
O objectivo desta experiência é o estudo do efeito fotoeléctrico e a determinação da constante de Planck, usando 5 leds de cores diferentes e intensidade regulável a incidir sobre uma célula fotoeléctrica.
Aparato Experimental
A célula fotoeléctrica pertence ao aparato da PASCO AP-9368, é do tipo condensador onde uma das placas emite os foto-electrões. À medida que os fotoelectrões são emitidos a diferença de potencial aos terminais da fotocélula aumenta. Para cada comprimento de onda detectado produz um potencial segundo o efeito fotoeléctrico.
Os terminais da fotocélula são ligados á terra após feitas as medidas por forma a descarregar o circuito.
Os leds têm espectros e intensidades diferentes por isso o tempo necessário para atingir o tensão terminal depende do led utilizado.
| Cor | Frequência (THz) | Comprimento de onda (nm) |
|---|---|---|
| Azul.ab | 638.7 | 469.70 |
| Azul | 684.6 | 438.20 |
| Vermelho | 482.2 | 622.21 |
| Amarelo | 514.4 | 583.16 |
| Verde | 530.8 | 565.22 |
Protocolo
Segundo o efeito fotoeléctrico, o numero de fotoelectrões emitidos por unidade de tempo duplica quando a intesidade da luz duplica. (comportamento corpuscular da luz)
- Escolher a cor a incidir sobre a fotocélula.
- Tome nota da tensão de paragem e determine o tempo necessário para atingir a tensão máxima.
- Repita passo 2 para diferentes intensidades.
| Cor #1 __________(nome) | Transmissão (%) | Potencial paragem (V) | Tempo de carga (s) |
|---|---|---|---|
| 100 | |||
| 80 | |||
| 60 | |||
| 40 | |||
| 20 |
A energia cinética dos fotoelectrões depende apenas da frequência da luz. Quanto maior for a frequência da luz, maior é a energia.
- Obtenha as tensões de paragem para diferentes cores.
- Fazer um ajuste linear ao gráfico Tensão vs. Frequência e obtenha a constante de Planck.
| Cor (nome) | Frequência (Hz) | Potencial paragem (V) |
|---|---|---|
Protocolo Avançado
- Calcule a constante de tempo da montagem.
- Encontre os valores esperados do comprimento de onda apartir dos espectros dos leds.
- Refaça o gráfico tensão vs frequência com barras de erro.
Nota: Utilizou-se um ADC 12bit no intervalo de 0V a 5V.
Princípios Teóricos
Efeito Fotoeléctrico
O efeito foto-eléctrico consiste na emissão de electrões da superfície de um metal quando este é iluminado por luz de uma dada frequência (\( \nu \)). Um fotão de energia \( E = h \nu \) ao incidir no metal transfere a sua energia a um electrão pertencente a um dos átomos na rede cristalina do metal. A emissão de electrões do metal é muito dependente da frequência da luz incidente. Para cada metal, existe uma frequência critica, \( \nu _0 \), tal que para luz incidente com frequência inferior não há foto-electrões arrancados. Por outro lado, para frequências superiores, a energia dos foto-electrões emitidos aumenta linearmente com a energia dos fotões incidentes. A intensidade da luz incidente afecta somente o número de foto-electrões emitidos, mas não a sua energia, contrariamente ao que seria de esperar na teoria clássica da radiação. Einstein propôs a seguinte explicação para o fenómeno: a luz é transportada por fotões com uma dada energia E associada à frequência da luz \( \nu \):
\[ E = h \times \nu \]
em que h é a constante de Planck. O efeito foto-eléctrico deve-se a uma colisão do fotão com o electrão, em que aquele transmite a este toda a sua energia. Tendo em conta que a energia de um electrão no vazio e dentro do metal é diferente (mais elevada no vazio), só se verifica efeito foto-eléctrico se a energia transmitida pelo fotão for superior à diferença entre estas duas energias (ver Fig. 1). Assim, a energia com que o electrão abandona o metal é igual à energia do fotão menos a energia "gasta" para o electrão abandonar o metal:
\[ E = h \times \nu - e \times \phi, \]
em que e é a carga do electrão e \( \phi \) é a diferença de workfunction. Tal como foi anteriormente enunciado, à medida que a frequência da luz incidente decresce, os fotões têm menos energia, e a partir de uma frequência critica \( \nu _0 \) não são emitidos mais foto-electrões. Neste caso, \( E _{max} = 0 \) e da Eq. l tiramos
\[ h \nu _0 = e \phi \quad ou \quad \nu _0 = \frac{e}{h} \phi \]
Efeito Fotoeléctrico
Uma célula foto-eléctrica é um dispositivo onde a luz incidente sobre uma superfície metálica (cátodo) excita electrões que vão ser colectados numa superfície metálica concêntrica (ânodo), tal como exemplificado na figura, e que na prática é um condensador semi-cilíndrico de capacidade muito baixa. Ligando o ânodo e o cátodo por um circuito externo, podemos medir a corrente produzida pelos foto-electrões. No caso mais genérico, a energia cinética máxima dos foto-electrões emitidos é determinada aplicando um potencial de paragem, Vc entre o ânodo e o cátodo de modo a impedir que os foto-electrões emitidos pelo cátodo atinjam o ânodo. Deste modo, deixa de fluir corrente no circuito.
A célula inicialmente tem aplicada a tensão da fonte, aproximadamente 9V uma vez que o condensador é descarregado no início da experiência (é efectuado um curto-circuito aos seus terminais). Como a célula está em série com o condensador, este vai carregando à medida que são gerados foto-electrões, criando uma corrente eléctrica no circuito que atravessa a célula. À medida que o condensador carrega, aumenta a diferença de potencial aos seus terminais, o que obriga a diminuir a tensão aos terminais da célula (note que \( V_{bat} = V_{Cond} + V_{célula} = constante \)). Quando a diferença de potencial nas placas da célula for igual a \( V_c = \frac{h \times \nu - e \times \phi}{e} \), deixa de fluir corrente no circuito e o condensador passa a ter uma tensão constante aos seus terminais.
Conhecendo dois ou mais valores dessa tensão para determinadas frequências [1] pode-se efectuar uma regressão linear e determinar não só \( \phi \) mas também a constante de Planck. No gráfico seguinte esquematizamos a dependência da tensão de paragem V em função da frequência da luz incidente para um dado metal. A função em causa corresponde a uma recta de declive \( \frac{h}{e} \) e coeficiente na origem \( \phi \).
Elementos Históricos
Em 1921 foi atribuído a Albert Einstein o Prémio Nobel da Física pelas suas descobertas no efeito fotoeléctrico.