Difference between revisions of "Determinação da Constante de Planck"
| (68 intermediate revisions by 4 users not shown) | |||
| Line 1: | Line 1: | ||
=Descrição da Experiência= | =Descrição da Experiência= | ||
| − | O objectivo desta experiência é o estudo do efeito fotoeléctrico e a determinação da constante de Planck, usando 5 leds de cores diferentes e intensidade regulável a incidir sobre uma célula fotoeléctrica. | + | O objectivo desta experiência é o estudo do efeito fotoeléctrico e a determinação da constante de Planck, usando 5 leds de cores diferentes (vários comprimentos de onda) e intensidade regulável a incidir sobre uma célula fotoeléctrica. |
| + | |||
| + | |||
| + | <div class="toccolours mw-collapsible mw-collapsed" style="width:420px"> | ||
| + | '''Ligações''' | ||
| + | <div class="mw-collapsible-content"> | ||
| + | |||
| + | *Video: Em breve | ||
| + | *Laboratório: [https://elab.vps.tecnico.ulisboa.pt:8000/execution/create/5/5 free.elab] | ||
| + | *Sala de controlo: Planck | ||
| + | *Nivel: ** | ||
| + | |||
| + | </div> | ||
| + | </div> | ||
=Aparato Experimental= | =Aparato Experimental= | ||
[[File:Espectro_dos_leds.png|thumb|alt=Espectro dos Leds|Figura 1: Espectro dos leds.]] | [[File:Espectro_dos_leds.png|thumb|alt=Espectro dos Leds|Figura 1: Espectro dos leds.]] | ||
| − | + | [[File:PlanckDoubleLine.png|thumb|Figura 2: Duplo fit da caracteristica dum dos leds azuis.]] | |
| − | + | A célula fotoeléctrica pertence ao aparato da PASCO AP-9368, é do tipo condensador onde uma das placas emite os fotoelectrões. À medida que os fotoelectrões são emitidos e acumulados na outra armadura do condensador, gera-se uma diferença de potencial aos terminais da fotocélula. Este potencial aumenta com o tempo até atingir um valor máximo. Nesse instante o condensador cessa de carregar (os fotoelectrões deixam de ter energia cinética suficiente para atingir essa segunda armadura devido ao potencial de travagem). Para cada comprimento de onda utilizado produz-se consequentemente um potêncial final diferente. | |
| − | Os | + | Os terminais da fotocélula são ligados à terra após as medidas serem concluídas para, no início da experiência seguinte, o condensador estar descarregado. Isto permite a determinação correcta do tempo de carga em função da intensidade da radiação (não confundir com a energia do fotoeletrão). |
| − | + | A eficiência quântica de cada led depende da sua cor (são fabricados com diferentes materiais) e, por consequência, a intensidade também o será. Isto implica que o tempo necessário para atingir a tensão final vai depender deste factores. | |
| − | |||
| − | + | Os gráficos da figura 1 mostram os espetros de cada led que estão tabelados em maior detalhe nos ficheiros de texto da tabela 1. | |
| − | |||
| − | + | Note-se que o comprimento de onda da emissão de radiação de cada led depende da temperatura da junção que por sua vez dependerá não só da temperatura ambiente como também da corrente que o atravessa. No entanto este efeito (desvio para o vermelho) é mais pronunciado em leds de cor quente (verdes-vermelhos) do que os leds azuis, pelo que o cálculo da constante de Planck poderá sofrer um desvio. | |
| − | + | De notar que um dos leds azuis apresenta uma característica modelada por uma dupla risca apenas identificável com um ajuste gaussiano duplo (pelo que o comprimento de onda a considerar será 429 e 469 nm, ver Figura 2) | |
{| border="1" style="text-align: center;" | {| border="1" style="text-align: center;" | ||
| − | |+ Tabela 1 – | + | |+ Tabela 1 – Valores máximos do espectro de cada led; este valor deve ser utilizado tendo em conta a dispersão do comprimento de onda (ver ficheiro de dados) obtidos com 7mA. |
|- | |- | ||
!Cor | !Cor | ||
| − | !Frequência ( | + | !Frequência (THz) |
| − | !Comprimento de onda | + | !Comprimento de onda (nm) |
| + | !Espectros dos leds | ||
|- | |- | ||
| − | | | + | |Azul.ab |
| − | | | + | |638.7 |
| − | | | + | |469.70 |
| − | | | + | |[[File:Espectro_Azul.ab.txt|Azul.ab]] |
| − | | | ||
| − | |||
| − | |||
|- | |- | ||
|Azul | |Azul | ||
| − | |6. | + | |684.6 |
| − | | | + | |438.20* |
| + | |[[File:Espectro_Azul.txt|Azul]] | ||
|- | |- | ||
| − | | | + | |Vermelho |
| − | | | + | |482.2 |
| − | | | + | |622.21 |
| + | |[[File:Espectro_Vermelho.txt|Vermelho]] | ||
|- | |- | ||
|Amarelo | |Amarelo | ||
| − | | | + | |514.4 |
| − | | | + | |583.16 |
| + | |[[File:Example.txt|Amarelo]] | ||
| + | |- | ||
| + | |Verde | ||
| + | |530.8 | ||
| + | |565.22 | ||
| + | ||[[File:Espectro_Verde.txt|Verde]] | ||
|} | |} | ||
| + | =Protocolo= | ||
| + | Segundo o efeito fotoeléctrico, o número de fotoelectrões emitidos por unidade de tempo duplica quando a intesidade da luz duplica (comportamento corpuscular da luz). | ||
| − | + | Procedimento: | |
| − | |||
| − | |||
| − | + | #Escolher a cor a incidir sobre a fotocélula. | |
| − | + | #Tome nota da tensão de paragem e determine o tempo necessário para atingir a tensão máxima. | |
| − | # | + | #Repita passo 2 para diferentes intensidades. |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | # | ||
| − | # Repita | ||
| − | |||
| − | |||
| Line 112: | Line 79: | ||
|- | |- | ||
!Cor #1 __________(nome) | !Cor #1 __________(nome) | ||
| − | ! | + | !Intensidade (%) |
!Potencial paragem (V) | !Potencial paragem (V) | ||
!Tempo de carga (s) | !Tempo de carga (s) | ||
| Line 140: | Line 107: | ||
| | | | ||
| | | | ||
| + | |} | ||
| + | |||
| + | |||
| + | A energia cinética dos fotoelectrões depende apenas da frequência da luz. Quanto maior for a frequência da luz, maior é a energia. | ||
| + | |||
| + | #Obtenha as tensões de paragem para diferentes cores. | ||
| + | #Desenha o gráfico Tensão vs. Frequência. Faça um ajuste dos pontos a \( V = \frac{h}{e} \nu - \frac{W_0}{e} \) e obtenha a constante de Planck. | ||
| + | |||
| + | |||
| + | {| border="1" style="text-align: center;" | ||
| + | |+ Exemplo de uma tabela | ||
|- | |- | ||
| − | !Cor | + | !Cor (nome) |
| − | ! | + | !Frequência (THz) |
!Potencial paragem (V) | !Potencial paragem (V) | ||
| − | |||
|- | |- | ||
| | | | ||
| − | | | + | | |
| − | | | + | | |
| − | |||
|- | |- | ||
| + | | | ||
| | | | ||
| − | | | + | | |
| − | |||
| − | |||
|- | |- | ||
| + | | | ||
| | | | ||
| − | | | + | | |
| − | |||
| − | |||
|- | |- | ||
| − | | | + | | |
| − | |||
| | | | ||
| | | | ||
|- | |- | ||
| | | | ||
| − | | | + | | |
| − | |||
| | | | ||
|} | |} | ||
| + | |||
| + | =Protocolo Avançado= | ||
| + | |||
| + | #Observe o processo de carga carga da fotocélula para diferentes intensidades. | ||
| + | #Encontre os valores esperados do comprimento de onda apartir dos espectros dos leds. | ||
| + | #Utilize-os para um novo fit e compare os resultados | ||
| + | #Refaça o gráfico tensão vs frequência com as barras de erro. | ||
| + | |||
| + | Nota: Utilizou-se um ADC 12bit no intervalo de 0V a 5V. | ||
=Princípios Teóricos= | =Princípios Teóricos= | ||
| − | ==Efeito | + | ==Efeito Fotoelétrico== |
| − | O efeito | + | O efeito fotoelétrico consiste na emissão de eletrões da superfície de um metal quando este é iluminado por luz de uma dada frequência (\( \nu \)). Um fotão de energia \( E = h \nu \), ao incidir no metal, transfere-a a um eletrão pertencente a um dos átomos na rede cristalina do metal. A emissão de eletrões do metal é muito dependente da frequência da luz incidente. Para cada metal, existe uma frequência critica, \( \nu _0 \), tal que para luz incidente com frequência inferior não há foto-electrões arrancados. Por outro lado, para frequências superiores, a energia dos foto-electrões emitidos aumenta linearmente com a energia dos fotões incidentes. A intensidade da luz incidente afecta somente o número de fotoeletrões emitidos, mas não a sua energia (contrariamente ao que seria de esperar na teoria clássica da radiação). |
Einstein propôs a seguinte explicação para o fenómeno: a luz é transportada por fotões com uma dada energia E associada à frequência da luz \( \nu \): | Einstein propôs a seguinte explicação para o fenómeno: a luz é transportada por fotões com uma dada energia E associada à frequência da luz \( \nu \): | ||
| − | + | <math> | |
| − | E = h | + | E = h \nu |
| − | + | </math> | |
| − | em que ''h'' é a constante de Planck. O efeito foto-eléctrico deve-se a uma colisão do fotão com o electrão, em que | + | em que ''h'' é a constante de Planck. O efeito foto-eléctrico deve-se a uma colisão do fotão com o electrão, em que o primeiro transmite ao segundo toda a sua energia. Tendo em conta que a energia de um electrão no vazio e dentro do metal é diferente (mais elevada no vazio), só se verifica efeito foto-eléctrico se a energia transmitida pelo fotão fôr superior à diferença entre estas duas energias (ver Fig. 1). Assim, a energia com que o electrão abandona o metal é igual à energia do fotão menos a energia "gasta" para o electrão abandonar o metal: |
| − | + | <math> | |
| − | E = h | + | E = h \nu - e \phi |
| − | + | </math> | |
em que ''e'' é a carga do electrão e \( \phi \) é a diferença de ''workfunction''. | em que ''e'' é a carga do electrão e \( \phi \) é a diferença de ''workfunction''. | ||
| − | Tal como foi anteriormente enunciado, à medida que a frequência da luz incidente decresce, os fotões têm menos energia, e a partir de uma frequência critica \( \nu _0 \) não são emitidos mais foto-electrões. Neste caso, \( E _{max} = 0 \) e | + | Tal como foi anteriormente enunciado, à medida que a frequência da luz incidente decresce, os fotões têm menos energia, e a partir de uma frequência critica \( \nu _0 \) não são emitidos mais foto-electrões. Neste caso, \( E _{max} = 0 \) e então: |
| − | + | <math> | |
h \nu _0 = e \phi \quad ou \quad \nu _0 = \frac{e}{h} \phi | h \nu _0 = e \phi \quad ou \quad \nu _0 = \frac{e}{h} \phi | ||
| − | + | </math> | |
[[File:Plank-teo1.png|thumb]] | [[File:Plank-teo1.png|thumb]] | ||
| − | + | ==A célula fotoelectrica== | |
| − | == | + | Uma célula fotoelétrica é um dispositivo onde a luz incidente sobre uma superfície metálica (cátodo) excita electrões que vão ser colectados numa superfície metálica concêntrica (ânodo), tal como exemplificado na figura (na prática, é um condensador semi-cilíndrico de capacidade muito baixa). Ligando o ânodo e o cátodo por um circuito externo, podemos medir a corrente produzida pelos foto-electrões. No caso mais genérico, a energia cinética máxima dos foto-electrões emitidos é determinada aplicando um potêncial de paragem Vc entre o ânodo e o cátodo de modo a impedir que os foto-electrões emitidos pelo cátodo atinjam o ânodo. Deste modo, quando deixar de fluir corrente no circuito, teremos o valor da corrente desejado. |
| − | Uma célula | ||
[[File:Plank-celula1.png|thumb]] | [[File:Plank-celula1.png|thumb]] | ||
| − | + | Inicialmente, é aplicada à célula a tensão da fonte (aproximadamente 9V, uma vez que o condensador é descarregado no início da experiência, efectuado um curto-circuito aos seus terminais). Como a célula está em série com o condensador, este vai carregando à medida que são gerados foto-electrões, criando uma corrente eléctrica no circuito que atravessa a célula. À medida que o condensador carrega, aumenta a diferença de potencial aos seus terminais, o que obriga a diminuir a tensão aos terminais da célula (note-se que \( V_{bat} = V_{Cond} + V_{célula} = constante \)). Quando a diferença de potêncial nas placas da célula fôr igual a \( V_c = \frac{h \nu - e \phi}{e} \), deixa de fluir corrente no circuito e o condensador passa a ter uma tensão constante aos seus terminais. | |
| − | Conhecendo dois ou mais valores dessa tensão para determinadas frequências | + | Conhecendo dois ou mais valores dessa tensão para determinadas frequências pode-se efectuar uma regressão linear e determinar não só \( \phi \) mas também a constante de Planck. No gráfico seguinte esquematizamos a dependência da tensão de paragem V em função da frequência da luz incidente para um dado metal. A função em causa corresponde a uma recta de declive \( \frac{h}{e} \) e coeficiente na origem \( \phi \). |
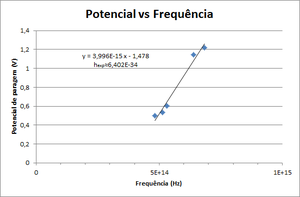
| − | [[File: | + | [[File:Constante de Planck.png|thumb|alt=Constante de Planck|Tensão vs. Pico de frequência da luz]] |
| + | =Elementos Históricos= | ||
| + | Em 1921 foi atribuído a Albert Einstein o Prémio Nobel da Física pelas suas descobertas relativas ao efeito fotoeléctrico. | ||
| − | = | + | =Ligações= |
| − | + | *[[Determination of Planck's Constant | Versão em Inglês (English Version)]] | |
Latest revision as of 13:13, 22 November 2022
Contents
Descrição da Experiência
O objectivo desta experiência é o estudo do efeito fotoeléctrico e a determinação da constante de Planck, usando 5 leds de cores diferentes (vários comprimentos de onda) e intensidade regulável a incidir sobre uma célula fotoeléctrica.
Ligações
- Video: Em breve
- Laboratório: free.elab
- Sala de controlo: Planck
- Nivel: **
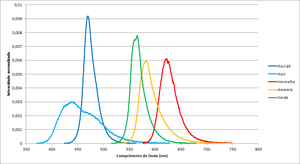
Aparato Experimental
A célula fotoeléctrica pertence ao aparato da PASCO AP-9368, é do tipo condensador onde uma das placas emite os fotoelectrões. À medida que os fotoelectrões são emitidos e acumulados na outra armadura do condensador, gera-se uma diferença de potencial aos terminais da fotocélula. Este potencial aumenta com o tempo até atingir um valor máximo. Nesse instante o condensador cessa de carregar (os fotoelectrões deixam de ter energia cinética suficiente para atingir essa segunda armadura devido ao potencial de travagem). Para cada comprimento de onda utilizado produz-se consequentemente um potêncial final diferente.
Os terminais da fotocélula são ligados à terra após as medidas serem concluídas para, no início da experiência seguinte, o condensador estar descarregado. Isto permite a determinação correcta do tempo de carga em função da intensidade da radiação (não confundir com a energia do fotoeletrão).
A eficiência quântica de cada led depende da sua cor (são fabricados com diferentes materiais) e, por consequência, a intensidade também o será. Isto implica que o tempo necessário para atingir a tensão final vai depender deste factores.
Os gráficos da figura 1 mostram os espetros de cada led que estão tabelados em maior detalhe nos ficheiros de texto da tabela 1.
Note-se que o comprimento de onda da emissão de radiação de cada led depende da temperatura da junção que por sua vez dependerá não só da temperatura ambiente como também da corrente que o atravessa. No entanto este efeito (desvio para o vermelho) é mais pronunciado em leds de cor quente (verdes-vermelhos) do que os leds azuis, pelo que o cálculo da constante de Planck poderá sofrer um desvio.
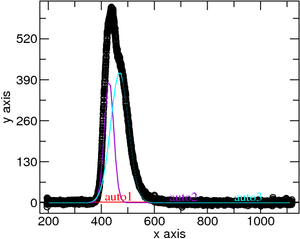
De notar que um dos leds azuis apresenta uma característica modelada por uma dupla risca apenas identificável com um ajuste gaussiano duplo (pelo que o comprimento de onda a considerar será 429 e 469 nm, ver Figura 2)
| Cor | Frequência (THz) | Comprimento de onda (nm) | Espectros dos leds |
|---|---|---|---|
| Azul.ab | 638.7 | 469.70 | File:Espectro Azul.ab.txt |
| Azul | 684.6 | 438.20* | File:Espectro Azul.txt |
| Vermelho | 482.2 | 622.21 | File:Espectro Vermelho.txt |
| Amarelo | 514.4 | 583.16 | File:Example.txt |
| Verde | 530.8 | 565.22 | File:Espectro Verde.txt |
Protocolo
Segundo o efeito fotoeléctrico, o número de fotoelectrões emitidos por unidade de tempo duplica quando a intesidade da luz duplica (comportamento corpuscular da luz).
Procedimento:
- Escolher a cor a incidir sobre a fotocélula.
- Tome nota da tensão de paragem e determine o tempo necessário para atingir a tensão máxima.
- Repita passo 2 para diferentes intensidades.
| Cor #1 __________(nome) | Intensidade (%) | Potencial paragem (V) | Tempo de carga (s) |
|---|---|---|---|
| 100 | |||
| 80 | |||
| 60 | |||
| 40 | |||
| 20 |
A energia cinética dos fotoelectrões depende apenas da frequência da luz. Quanto maior for a frequência da luz, maior é a energia.
- Obtenha as tensões de paragem para diferentes cores.
- Desenha o gráfico Tensão vs. Frequência. Faça um ajuste dos pontos a \( V = \frac{h}{e} \nu - \frac{W_0}{e} \) e obtenha a constante de Planck.
| Cor (nome) | Frequência (THz) | Potencial paragem (V) |
|---|---|---|
Protocolo Avançado
- Observe o processo de carga carga da fotocélula para diferentes intensidades.
- Encontre os valores esperados do comprimento de onda apartir dos espectros dos leds.
- Utilize-os para um novo fit e compare os resultados
- Refaça o gráfico tensão vs frequência com as barras de erro.
Nota: Utilizou-se um ADC 12bit no intervalo de 0V a 5V.
Princípios Teóricos
Efeito Fotoelétrico
O efeito fotoelétrico consiste na emissão de eletrões da superfície de um metal quando este é iluminado por luz de uma dada frequência (\( \nu \)). Um fotão de energia \( E = h \nu \), ao incidir no metal, transfere-a a um eletrão pertencente a um dos átomos na rede cristalina do metal. A emissão de eletrões do metal é muito dependente da frequência da luz incidente. Para cada metal, existe uma frequência critica, \( \nu _0 \), tal que para luz incidente com frequência inferior não há foto-electrões arrancados. Por outro lado, para frequências superiores, a energia dos foto-electrões emitidos aumenta linearmente com a energia dos fotões incidentes. A intensidade da luz incidente afecta somente o número de fotoeletrões emitidos, mas não a sua energia (contrariamente ao que seria de esperar na teoria clássica da radiação). Einstein propôs a seguinte explicação para o fenómeno: a luz é transportada por fotões com uma dada energia E associada à frequência da luz \( \nu \):
[math] E = h \nu [/math]
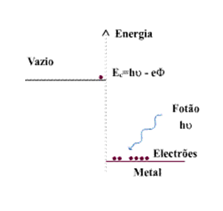
em que h é a constante de Planck. O efeito foto-eléctrico deve-se a uma colisão do fotão com o electrão, em que o primeiro transmite ao segundo toda a sua energia. Tendo em conta que a energia de um electrão no vazio e dentro do metal é diferente (mais elevada no vazio), só se verifica efeito foto-eléctrico se a energia transmitida pelo fotão fôr superior à diferença entre estas duas energias (ver Fig. 1). Assim, a energia com que o electrão abandona o metal é igual à energia do fotão menos a energia "gasta" para o electrão abandonar o metal:
[math] E = h \nu - e \phi [/math]
em que e é a carga do electrão e \( \phi \) é a diferença de workfunction. Tal como foi anteriormente enunciado, à medida que a frequência da luz incidente decresce, os fotões têm menos energia, e a partir de uma frequência critica \( \nu _0 \) não são emitidos mais foto-electrões. Neste caso, \( E _{max} = 0 \) e então:
[math] h \nu _0 = e \phi \quad ou \quad \nu _0 = \frac{e}{h} \phi [/math]
A célula fotoelectrica
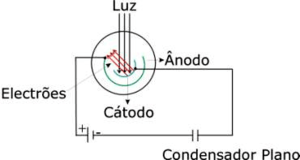
Uma célula fotoelétrica é um dispositivo onde a luz incidente sobre uma superfície metálica (cátodo) excita electrões que vão ser colectados numa superfície metálica concêntrica (ânodo), tal como exemplificado na figura (na prática, é um condensador semi-cilíndrico de capacidade muito baixa). Ligando o ânodo e o cátodo por um circuito externo, podemos medir a corrente produzida pelos foto-electrões. No caso mais genérico, a energia cinética máxima dos foto-electrões emitidos é determinada aplicando um potêncial de paragem Vc entre o ânodo e o cátodo de modo a impedir que os foto-electrões emitidos pelo cátodo atinjam o ânodo. Deste modo, quando deixar de fluir corrente no circuito, teremos o valor da corrente desejado.
Inicialmente, é aplicada à célula a tensão da fonte (aproximadamente 9V, uma vez que o condensador é descarregado no início da experiência, efectuado um curto-circuito aos seus terminais). Como a célula está em série com o condensador, este vai carregando à medida que são gerados foto-electrões, criando uma corrente eléctrica no circuito que atravessa a célula. À medida que o condensador carrega, aumenta a diferença de potencial aos seus terminais, o que obriga a diminuir a tensão aos terminais da célula (note-se que \( V_{bat} = V_{Cond} + V_{célula} = constante \)). Quando a diferença de potêncial nas placas da célula fôr igual a \( V_c = \frac{h \nu - e \phi}{e} \), deixa de fluir corrente no circuito e o condensador passa a ter uma tensão constante aos seus terminais.
Conhecendo dois ou mais valores dessa tensão para determinadas frequências pode-se efectuar uma regressão linear e determinar não só \( \phi \) mas também a constante de Planck. No gráfico seguinte esquematizamos a dependência da tensão de paragem V em função da frequência da luz incidente para um dado metal. A função em causa corresponde a uma recta de declive \( \frac{h}{e} \) e coeficiente na origem \( \phi \).
Elementos Históricos
Em 1921 foi atribuído a Albert Einstein o Prémio Nobel da Física pelas suas descobertas relativas ao efeito fotoeléctrico.