Boyle-Mariotte Law
Contents
Experiment Description
The purpose of this experiment is to verify the relation \( p \propto \frac{1}{V} \) (i.e., pressure and volume are inversely proportional) of a gas during isothermal expansion or compression.
Links
- Video: rtsp://elabmc.ist.utl.pt/pv.sdp
- Laboratory: Basic in e-lab.ist.eu[1]
- Control room: pv
- Grade: **
<swf height="270" width="510">http://www.elab.tecnico.ulisboa.pt/anexos/descricoes-flash/BoyleMariottePV.swf</swf>
Who likes this idea
Experimental Apparatus
The apparatus is composed by a cylinder (5 ml syringe) filled with air, whose plunger is displaced by a servo motor.
It is possible to choose the compression/expansion limits of the chamber and measure the air pressure and volume inside it during the plunger's motion. The speed at which the transformation occurs can also be specified by choosing the time between samples.
Protocol
The user must specify the initial and final volume, the number of samples and time interval between them. This last option indirectly defines the speed at which the transformation occurs.
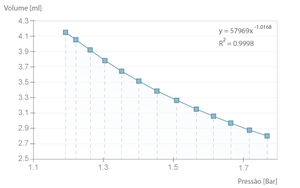
If the experiment is executed with a long time interval between samples, the transformation is close to isothermal. That means the air temperature inside the syringe doesn't change and the Boyle-Mariotte Law is applicable.
The example bellow is one such case where we can verify that the product \( pV \) is, in average, \( 49,3 \pm 0,3 l.kPa \), close to the theoretical value of \( nRT \) (where \( n = 2 \times 10 ^{-4} mol\), equivalent to the full syringe volume at rest \( 5 ml \), PTN).
If the time between samples is decreased (i.e. the process is faster), the transformation is no longer isothermal and becomes slightly adiabatic, because there is not enough time for the heat exchange between the inside of the cylinder and the environment. This way, the compression no longer follows the Boyle-Mariotte Law, a fact that is clearly demonstrated by the deviation from the power function, which would be \( ^3/_5 \) in the ideal case (\( \gamma ^{-1} = \frac{c_v}{c_p} \)).
It is difficult to obtain a fast enough compression to achieve this value, since thermalization occurs quickly (in the order of the sound speed). However this can be used to study how the transformation speed influences the deviation between the experimental data and the Boyle-Mariotte Law.
Advanced Protocol
With a high enough time between samples, it is also possible to determine the Ideal Gas Constant, if we consider room temperature to be 22ºC.
Procedure:
- Run the experiment with about 20 acquisitions, maximum extension between initial and final volume and maximum acquisition time allowed (we are trying to achieve an isothermal transformation).
- Fit the experimental data to a \( a x ^b \) type function and find the proportion constant (which will equal \( nRT \)).
- Assume the room temperature to be 22ºC. Determine the amount of substance (in mole) present at the inicial stage of the experiment ( \( 5 ml \) of air at NTP conditions). Find R.
- Compare the R value that was found through this method with the one found through the average product of \( pV \) (using a math software, determine the product between p and V for each line and then find the average).
- Find one last estimate for R setting the exponent at -1 (i.e., fitting the data to a \( a x ^{-1} \) function).