Difference between revisions of "Boyle-Mariotte Law"
| (5 intermediate revisions by 3 users not shown) | |||
| Line 18: | Line 18: | ||
<swf height="270" width="510">http://www.elab.tecnico.ulisboa.pt/anexos/descricoes-flash/BoyleMariottePV.swf</swf> | <swf height="270" width="510">http://www.elab.tecnico.ulisboa.pt/anexos/descricoes-flash/BoyleMariottePV.swf</swf> | ||
| + | |||
| + | =Who likes this idea= | ||
| + | [[File:EscolherCiencia.png|link=http://www.cienciaviva.pt/escolherciencia/|border|179px|border|179px]] | ||
| + | [[File:ECB Logo.png|link=http://www.externatobenedita.net/|border|179px|border|179px]] | ||
| + | [[File:Logo_alberto_cores.jpg|link=http://www.es-al-berto.com/|border|120px|border|120px]] | ||
| + | [[File:LogoAEA_800x132.jpg|link=http://aealvalade.edu.pt/|border|280px|border|280px]] | ||
| + | |||
| + | |||
| + | This idea is the result of the PEC26 contract with Ciência Viva - The portuguese Agency for Cientific and technological Culture and its objectives are (i) sharing (through the internet) existing experimental setups that some high-schools have but are not in use and (ii) promote teaching cience through the use of experimental activities. The automation of the experiment was made by IST students as part of the e-lab project. | ||
| + | |||
| + | The first school involved in this experiment were Escola Secundária Padre António Vieira, Alvalade/Lisboa and Externato Cooperativo da Benedita, Leiria. Escola Secundária Poeta Al Berto in Sines also colaborated. | ||
=Experimental Apparatus= | =Experimental Apparatus= | ||
| Line 42: | Line 53: | ||
=Advanced Protocol= | =Advanced Protocol= | ||
| − | With a high enough time between samples, | + | With a high enough time between samples we can consider the transformation to be isothermal (i.e. the temperature inside the seringe doesn't change). |
| + | |||
| + | With this, we can perform two adicional experiments. | ||
| + | |||
| + | ==Volume outside the seringe== | ||
| + | We can determine the volume of air between the seringe and the associated devices (like the purge valve and the tubes conected to the pressure sensor). | ||
| + | |||
| + | We consider a volume \( V_0 \) added to the seringe volume and do the following procedure: | ||
| + | # Run an experiments with a few samples (e.g. 20) with maximum diference between inicial and final volumes and maximum time between samples. | ||
| + | # Fit the resulting data to a \( p = a/(V+ V_0) \) type function and determine both \( V_0 \) and \( a \) (which will be equal to \(nRT\) ). | ||
| + | |||
| + | ==Ideal Gas Constant== | ||
| + | It is also possible to determine the Ideal Gas Constant, if we consider room temperature to be 22ºC. | ||
Procedure: | Procedure: | ||
| Line 50: | Line 73: | ||
# Compare the R value that was found through this method with the one found through the average product of \( pV \) (using a math software, determine the product between p and V for each line and then find the average). | # Compare the R value that was found through this method with the one found through the average product of \( pV \) (using a math software, determine the product between p and V for each line and then find the average). | ||
# Find one last estimate for R setting the exponent at -1 (i.e., fitting the data to a \( a x ^{-1} \) function). | # Find one last estimate for R setting the exponent at -1 (i.e., fitting the data to a \( a x ^{-1} \) function). | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
=Links= | =Links= | ||
*[[Lei de Boyle-Mariotte | Portuguese version (Versão em Português)]] | *[[Lei de Boyle-Mariotte | Portuguese version (Versão em Português)]] | ||
Latest revision as of 20:40, 15 August 2017
Contents
Experiment Description
The purpose of this experiment is to verify the relation \( p \propto \frac{1}{V} \) (i.e., pressure and volume are inversely proportional) of a gas during isothermal expansion or compression.
Links
- Video: rtsp://elabmc.ist.utl.pt/pv.sdp
- Laboratory: Basic in e-lab.ist.eu[1]
- Control room: pv
- Grade: **
<swf height="270" width="510">http://www.elab.tecnico.ulisboa.pt/anexos/descricoes-flash/BoyleMariottePV.swf</swf>
Who likes this idea
This idea is the result of the PEC26 contract with Ciência Viva - The portuguese Agency for Cientific and technological Culture and its objectives are (i) sharing (through the internet) existing experimental setups that some high-schools have but are not in use and (ii) promote teaching cience through the use of experimental activities. The automation of the experiment was made by IST students as part of the e-lab project.
The first school involved in this experiment were Escola Secundária Padre António Vieira, Alvalade/Lisboa and Externato Cooperativo da Benedita, Leiria. Escola Secundária Poeta Al Berto in Sines also colaborated.
Experimental Apparatus
The apparatus is composed by a cylinder (5 ml syringe) filled with air, whose plunger is displaced by a servo motor.
It is possible to choose the compression/expansion limits of the chamber and measure the air pressure and volume inside it during the plunger's motion. The speed at which the transformation occurs can also be specified by choosing the time between samples.
Protocol
The user must specify the initial and final volume, the number of samples and time interval between them. This last option indirectly defines the speed at which the transformation occurs.
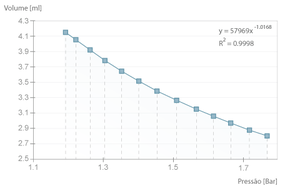
If the experiment is executed with a long time interval between samples, the transformation is close to isothermal. That means the air temperature inside the syringe doesn't change and the Boyle-Mariotte Law is applicable.
The example bellow is one such case where we can verify that the product \( pV \) is, in average, \( 49,3 \pm 0,3 l.kPa \), close to the theoretical value of \( nRT \) (where \( n = 2 \times 10 ^{-4} mol\), equivalent to the full syringe volume at rest \( 5 ml \), PTN).
If the time between samples is decreased (i.e. the process is faster), the transformation is no longer isothermal and becomes slightly adiabatic, because there is not enough time for the heat exchange between the inside of the cylinder and the environment. This way, the compression no longer follows the Boyle-Mariotte Law, a fact that is clearly demonstrated by the deviation from the power function, which would be \( ^3/_5 \) in the ideal case (\( \gamma ^{-1} = \frac{c_v}{c_p} \)).
It is difficult to obtain a fast enough compression to achieve this value, since thermalization occurs quickly (in the order of the sound speed). However this can be used to study how the transformation speed influences the deviation between the experimental data and the Boyle-Mariotte Law.
Advanced Protocol
With a high enough time between samples we can consider the transformation to be isothermal (i.e. the temperature inside the seringe doesn't change).
With this, we can perform two adicional experiments.
Volume outside the seringe
We can determine the volume of air between the seringe and the associated devices (like the purge valve and the tubes conected to the pressure sensor).
We consider a volume \( V_0 \) added to the seringe volume and do the following procedure:
- Run an experiments with a few samples (e.g. 20) with maximum diference between inicial and final volumes and maximum time between samples.
- Fit the resulting data to a \( p = a/(V+ V_0) \) type function and determine both \( V_0 \) and \( a \) (which will be equal to \(nRT\) ).
Ideal Gas Constant
It is also possible to determine the Ideal Gas Constant, if we consider room temperature to be 22ºC.
Procedure:
- Run the experiment with about 20 acquisitions, maximum extension between initial and final volume and maximum acquisition time allowed (we are trying to achieve an isothermal transformation).
- Fit the experimental data to a \( a x ^b \) type function and find the proportion constant (which will equal \( nRT \)).
- Assume the room temperature to be 22ºC. Determine the amount of substance (in mole) present at the inicial stage of the experiment ( \( 5 ml \) of air at NTP conditions). Find R.
- Compare the R value that was found through this method with the one found through the average product of \( pV \) (using a math software, determine the product between p and V for each line and then find the average).
- Find one last estimate for R setting the exponent at -1 (i.e., fitting the data to a \( a x ^{-1} \) function).