Interpretação quântica de três polarizadores
Jump to navigation
Jump to search
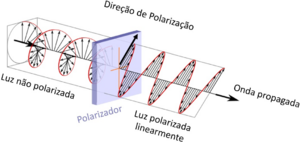
Vamos descrever o estado de polarização da luz como um vetor bidimensional, como ilustrado na figura. A luz polarizada verticalmente corresponde a um vetor apontando para cima (0, 1), horizontalmente corresponde a (1,0). Usamos a notação de Dirac para representar estes vectores, |V> e |H> respetivamente. Um vetor arbitrário é escrito como \(|α〉=cosα |V〉+sinα |H〉 \).
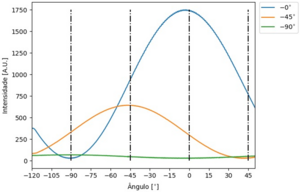
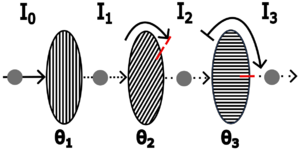
A mecânica quântica explica como calcular: 1) a probabilidade de transmissão desses estados através de um polarizador, 2) o estado à saída do polarizador. Quando o estado \(|V>\) passa pelo segundo polarizador, orientado a 45°, temos que: A probabilidade de transmissão é dada por
[math]
〖Prob=|〈V|P_(45°) |V〉|〗^2=1/2
[/math]