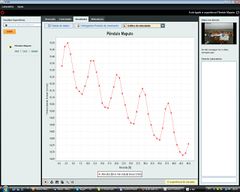
Péndulo mundial
Contents
Descripción
Los cohetes se lanzan al espacio desde las latitudes ecuatoriales. Esto se debe al hecho de que el peso aparente de los objetos se reduce gradualmente desde los polos hasta el ecuador. ¡Nos sentiremos más ligeros en el ecuador que en los polos!
Esta pequeña diferencia en el peso aparente permite que el mismo cohete lance cargas más pesadas en órbita si se lanza más cerca del ecuador. Por ejemplo, un cohete Soyuz que se lanza en órbita geoestacionaria desde la Guayana Francesa (5ºN) puede transportar 3 toneladas, mientras que solo será capaz de lanzar 1,7 toneladas de carga cuando se lance desde Baikonur, Kazajstán (46ºN).
El objetivo de este experimento es encontrar el valor de la gravedad "constante" a través de una constelación de péndulos colocados en varias latitudes y operados remotamente, a través de Internet, por cualquier persona.
Se espera que los países de la CPLP puedan contribuir a este esfuerzo, acercando a estudiantes, maestros y ciudadanos interesados.
Hay dos actividades diferentes que ocurren simultáneamente: (i) acceso, a través del laboratorio elecrónico, de los péndulos ubicados en diferentes latitudes y (ii) la construcción y operación local en las escuelas o en tu casa.
Lisboa, Ilhéus, Faro y Río de Janeiro fueron las primeras ciudades en contribuir a la red en enero de 2013, haciendo posible que ocurran los primeros ajustes de datos experimentales a la ecuación teórica dentro de nuestro proyecto que describe cómo la gravedad cambia con la latitud.
Si desea formar parte de la nueva red World Pendulum, contáctenos enviándonos un [mailto: wwwelab@ist.utl.pt email].
Enlaces
- Video Faro: rtsp: //elabmc.ist.utl.pt/worldpendulum_ccvalg.sdp
- Video Lisboa: rtsp: //elabmc.ist.utl.pt/worldpendulum_planetarium.sdp
- Video Ilhéus: rtsp: //elabmc.ist.utl.pt/worldpendulum_ilheus.sdp
- Video Río Janeiro: rtsp: //elabmc.ist.utl.pt/worldpendulum_puc.sdp
- Video Maputo: rtsp: //elabmc.ist.utl.pt/worldpendulum_maputo.sdp
- Video Santo Tomé: rtsp: //elabmc.ist.utl.pt/wp_saotome.sdp
- Laboratorio: Básico en e-lab.ist.eu
- Sala de control: Péndulo mundial
- Grado: *
A quién le gusta esta idea
Aparato experimental
El diseño del péndulo utilizado se basó en el diseño del Dr. Jodl [1]. Se hicieron algunos cambios menores para permitir que el mismo diseño se repita fácilmente en las escuelas secundarias. Los datos relativos a cada péndulo son los siguientes:
| Tamaños físicos por lugar | |||||
|---|---|---|---|---|---|
| Sitio | Latitud | Longitud | Altitud (m) | Longitud de la cuerda (mm) | Diámetro de la esfera (mm) |
| CCV_Algarve / Faro | 37º00'N | 7º56'W | 10 m | 2677mm +/- 0.5mm @ 23ºC | 80.5 +/- 1.0 mm |
| UESC / Ilhéus | 14º47'S | 39º10'W | 220m | 2705mm +/- 0.5mm @ 23ºC | 80.5 +/- 1.0 mm |
| Lisboa | 38º41'N | 9º12'W | 20m | 2677mm +/- 0.5mm @ 19ºC | 80.5 +/- 1.0 mm |
| Maputo | 25º56'S | 32º36'E | 80m | 2609.8mm +/- 0.5mm @ 27ºC | 80.5 +/- 1.0 mm |
| Santo Tomé | 0º21'N | 6º43'E | 50m | 2756.5mm +/- 0.5mm @ 29ºC | 81.8 +/- 0.5 mm |
| Praga - CTU | 50º5.47N | 14º24.97E | 150m | 2850mm +/- 0.5mm @ 25ºC | 80.15 +/- 0.5 mm |
| Barcelona - UPC | 41º24.6N | 2º13.12E | 55 | 2756.5mm +/- 0.5mm | 81.8mm |
| Río de Janeiro - PUC | 22º54.13S | 43º12W | 50 | 2826,0mm +/- 0.5mm | 81.6mm |
| Praia - UniCV | 14 ° 56 'N | 23 ° 31'W | 40 m | 2826,0mm +/- 0.5mm | 81.6mm |
| Bogotá - UniAndes | 4 ° 36 'N | 74 ° 3'W | 2650 m | 2815,3mm+/- 0.5mm | 82.0mm |
| Ciudad de Panamá - UTP | 9 ° 1.34 'N | 79 ° 31.92'W | 82 m | 2825mm +/- 0.5mm @ 28ºC | 81.9mm |
| Santiago - UChile | 33 ° 27.46 'S | 70 ° 39.79'W | 552 m | 2825mm +/- 0.5mm @ 27ºC | 81.9mm |
| Valparaíso - UTFSM | 9 ° 1.34 'N | 79 ° 31.92'W | 82 m | 2825mm +/- 0.5mm @ 28ºC | 81.9mm |
| Cantidades típicas | |
|---|---|
| Longitud de cadena (sin contar la esfera) | 2705mm +/- 0.5mm |
| Masa de esfera | 2kg +/- 75g |
| Diámetro de esfera | 81.2mm +/- 1.5mm |
| Cadena | Remanio (r) - Acero inoxidable (níquel cromo)- 0,4mm |
| Módulo de elasticidad de la cuerda | ~ 200GPa |
| Sistema de medición del período de oscilación | Microprocesador con 7,3728MHz - 30ppm de cristal+ láser + fotodiodo PIN |
| Alambre CTE (25-500ºC) (Coeficiente de expansión térmica) | ~ 14 x 10 -6 K -1 |
El aparato experimental se puede adaptar fácilmente a la operación humana, utilizando un buen cronómetro, para la ejecución local. Las estructuras de acero inoxidable pueden fabricarse en latón o bronce para facilitar el mecanizado. El cable utilizado puede ser reemplazado por un cable de acero para pesca deportiva y la masa puede ser reemplazada por un peso de entrenamiento de lanzamiento de pesas olímpico, que pesa 2 kg. Se debe usar una cinta de medición calibrada para medir la longitud del cable "," unos días después de ensamblar el aparato para permitir la expansión del cable ".
Socios locales
El péndulo [2], aunque uno de los sistemas más simples comúnmente estudiados, es uno de los más rico en términos de física.
Para construir un péndulo preciso, los factores más importantes son la medición precisa de la longitud del cable, su calidad y la de los soportes del péndulo. La selección de una masa entre 1 y 4 kg asegura que el error del período del péndulo sea lo suficientemente pequeño como para que se puedan detectar pequeños cambios de gravedad locales (menores del 0.1%), siempre que se use un cronómetro preciso para el cronometraje.
Se puede ensamblar un aparato local utilizando materiales fácilmente disponibles y los valores locales de "g" determinados usando dicho aparato se pueden comparar con los obtenidos a través de la constelación de péndulo remoto y el modelo teórico.
La recopilación de estos datos a través de una red social permitirá una descripción más precisa de cómo "g" varía en todo el mundo. El "Péndulo mundial" puede ser una red de colaboración importante para la difusión de la física en las escuelas.
Las instrucciones sobre cómo construir tal péndulo están disponibles en Precision Pendulum. La documentación del desarrollo y construcción de un péndulo está disponible en Precision Pendulum mientras que las instrucciones sobre cómo ensamblarlo están disponibles en Precision Pendulum Assembly.
Si desea formar parte de la nueva red World Pendulum, contáctenos enviándonos un [mailto: wwwelab@ist.utl.pt email].
Física
Determinar la aceleración de la gravedad en diferentes partes del mundo plantea preguntas sobre la importancia de los modelos en física. Es posible mostrar que la aceleración de la gravedad al nivel del mar cambia con la latitud y, por lo tanto, se necesita una corrección para cada ubicación individual. Este proceso nos permite desmitificar la ciencia y corregir el "mito urbano" existente en torno a algunas constantes físicas que solo son verdaderamente constantes cuando se realizan algunas aproximaciones. En este caso particular, mostraremos cómo la introducción de correcciones sucesivas a la "constante" de la gravedad conducirá a valores más cercanos a los obtenidos experimentalmente.
Modelo geofísico
El punto de partida es el valor constante de uso común de 9.81 ms -2 . Esto se obtiene al considerar que la Tierra es (i) una esfera (ii) que no está girando. Es trivial notar que este modelo, debido a la simetría de la forma esférica, no permite valores diferentes en diferentes ubicaciones. Esto cambia tan pronto como se tienen en cuenta la dinámica de rotación de la Tierra y la forma elipsoide (aplanamiento de los polos). Estos factores permiten que la gravedad cambie con la latitud, y de hecho, estos dos factores son los dos más importantes en este fenómeno, superando cualquier otro efecto, como (i) altitud, (ii) fuerzas de marea y (iii) composición del subsuelo .
Para demostrar estos aspectos más finos, la aceleración de la gravedad debe determinarse en varias latitudes alrededor del globo distantes entre sí. Usando los datos recopilados, los estudiantes pueden preguntarse qué tan "constante" es realmente el valor y mejorar su intuición de la gravedad.
Estudios experimentales
Variación con latitud
Como se ve, el primer estudio posible consiste en usar los péndulos remotos para obtener una medición de la aceleración de la gravedad local para cada ubicación en la que se basan. Al considerar (o no) varios factores, es posible ajustar los datos a un experimento Descripción de la Tierra utilizando armónicos esféricos (ecuación \ eqref {harmonica-esferica}). Este trabajo experimental puedese llevará a cabo utilizando la constelación de péndulo de e-lab y los péndulos de nuestro socio.
Determinación local
Siguiendo las instrucciones disponibles en este wiki - Precision_Pendulum - o usando cualquier otro tipo de diseño que resulte en un aparato riguroso, se construye un péndulo local. Entonces es posible realizar mediciones de la gravedad local, siempre que se use un buen cronómetro. Además, también es posible contribuir al enriquecimiento de la red mundial.
Estudio de mareas
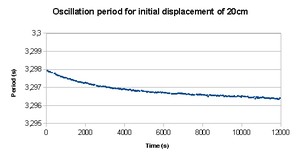
Usando un almanaque apropiado para la ubicación, puede obtener los tiempos de alineaciones particulares de Luna / Sol (luna llena, luna nueva, creciente creciente y gibosa creciente). Al trazar un gráfico que abarque varios meses, se puede intentar verificar y cuantificar la influencia de las fuerzas de marea y las alineaciones Luna / Sol en el peso aparente. Es posible intentar y verificar la correlación entre las fases de la Luna y los cambios en la medición de la gravedad local, haciendo un estudio de un mes o un año. Los efectos de las mareas están en el límite de detección por los péndulos de la constelación de e-lab. Para que el experimento tenga éxito, es necesario ser muy riguroso en el momento en que se realizan las corridas experimentales y algunas técnicas numéricas avanzadas, como la transformada de Fourier, deben emplearse para que la señal se extraiga de los datos.
Análisis de torsión de alambre
Quienes presten más atención notarán que la velocidad de la masa cambia debido a la torsión del alambre y debido a que la masa no es una esfera perfecta. Esto se ilustra en la imagen a la derecha. El péndulo puede estudiarse teniendo en cuenta el efecto de la torsión del alambre (para ello se recomienda el uso de las ecuaciones de Euler-Lagrange).
Movimiento circular uniformemente acelerado
La velocidad de la esfera en el punto más bajo de la trayectoria se determina midiendo cuánto tiempo se interrumpe el rayo láser. Conociendo el diámetro de la esfera, es trivial determinar la velocidad en el origen. A partir de esto, se puede calcular la energía cinética máxima y determinar la altura de lanzamiento del péndulo. El punto de lanzamiento calculado se puede comparar con el real.
CPLP como "proveedor de latitud"
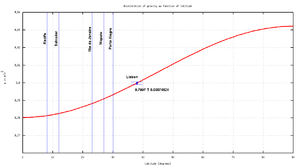
El idioma es un factor de nacionalidad importante ("Mi patria es el idioma portugués", F. Pessoa) y una forma sencilla de definir lo que se llama países hermanos ("países irmãos"). Solo cuatro idiomas se difunden en todo el mundo, siendo el portugués uno de ellos. La comunidad de habla portuguesa cubre latitudes de ~ 30S a ~ 40N, casi un tramo de 75º en el ecuador. Por lo tanto, los países CPLP pueden ayudar siendo "proveedores de latitud" (ver Figura).
Para llevar a cabo este experimento mundial, se necesitan al menos cuatro puntos espaciados para tener un ajuste adecuado. Pero debido a la fuerte no linealidad de la ecuación, se necesitan más puntos para proporcionar un ajuste adecuado, en particular en la "rodilla" cerca del ecuador de la Tierra. El propio Brasil puede proporcionar casi cuatro puntos cruciales cerca del ecuador (por ejemplo, Recife 8º, Salvador - 12º, Río de Janeiro - 23º, Porto Alegre - 30º) pero carece de puntos con una latitud donde la característica varía más fuertemente, la región casi lineal alrededor 30º a 60º, donde Portugal puede dar dos buenos puntos (por ejemplo, Porto - 37º y Faro - 41º). Mozambique puede contribuir con 27º (Maputo) y S. Tomé e Principe o Brasil son buenas opciones para cubrir el ecuador. Angola podría dar puntos complementarios a los adquiridos en Brasil, ya que la sensibilidad de la medición es más pronunciada cerca del ecuador y los polos.
Ajuste de datos
Referencias disponibles [2] [3] [4] [5] [6] [7] dan una muy buena descripción del modelo matemático necesario para ajustar los datos. Si se tienen en cuenta todos los factores principales, la gravedad en función de la latitud viene dada por:
<matemáticas> g_ {n} (\ varphi) = 9.780 326 772 \ times [1 + 0.005 302 33 \ cdot sin ^ {2} (\ varphi) - 0.000 005 89 \ cdot sin ^ {2} (2 \ varphi)] </math>
donde \ (\ varphi \) es la latitud. Esta expresión es una de las mejores aproximaciones experimentales y los resultados del acuerdo de estandarización para ajustar la superficie de referencia del Sistema Geodésico Mundial (WSG84) a un elipsoide con radio r 1 = 6378137m en el ecuador y r 2 = 6356752m de radio semi-menor polar. Esta fórmula tiene en cuenta el hecho de que la Tierra es un elipsoide y que hay un aumento adicional en la aceleración de la gravedad cuando uno se acerca a los polos, debido a una fuerza centrífuga más débil. Sin embargo, los estudiantes podrían obtener una aproximación no armónica de primer orden teniendo en cuenta solo la fuerza centrífuga. Luego, como un segundo paso, podrían incluir los otros dos errores principales, la fuerza centrífuga y el formato de elipsoide de la Tierra.
Las imágenes muestran la desviación esperada de la "aceleración constante de la Tierra", la aceleración real para cada latitud. Hemos trazado el punto ya obtenido con este aparato en Lisboa y las marcas sobre las latitudes esperadas para futuros socios. Por supuesto, estas aproximaciones no incluyen una fuente importante de desviación de los datos reales al modelo matemático, el error experimental, ya que no incluimos la fuente experimental de error. Sin embargo, esos errores sistemáticos podrían estar bajo la precisión esperada necesaria (0,1%) para la aproximación anterior si se considera un diseño cuidadoso del aparato. Sin embargo, esos errores deben discutirse en cursos avanzados y su peso debe probarse al considerar el péndulo real.
Notas históricas
La importancia del péndulo como base de los relojes y cronógrafos solo fue derrocada cuando la Royal Society convenció al parlamento inglés de crear un premio, que oscilaba entre 10k £ y 20k £ (equivalente hoy en día a más de 3.5M €), por la invención de un cronógrafo. eso no dependía de eso. La precisión temporal de los sistemas basados en péndulo solo se ve mejorada por los sistemas electrónicos modernos.
En la edad del descubrimiento, la longitud se determinó con un alto error, ya que los relojes y cronógrafos dependían de péndulos y estos eran muy sensibles a los barcos que se balanceaban, sufrían cambios en la frecuencia o incluso se detenían. La longitud local se calculó comparando la hora solar (u hora estelar) con la hora del reloj del barco.
Referencias
- ↑ World pendulum—a distributed remotely controlled laboratory (RCL) to measure the Earth's gravitational acceleration depending on geographical latitude, Grober S, Vetter M, Eckert B and Jodl H J, European Journal of Physics - EUR J PHYS , vol. 28, no. 3, pp. 603-613, 2007
- ↑ 2.0 2.1 Physics for scientists and engineers, 5th edition, Hardcourt College Publishers, R.Serway and R. Beichner, 2000
- ↑ http://rcl-munich.informatik.unibw-muenchen.de/
- ↑ Nelson, Robert; M. G. Olsson (February 1987). "The pendulum - Rich physics from a simple system". American Journal of Physics 54 (2): doi:10.1119/1.14703
- ↑ Pendulums in the Physics Education Literature: A Bibliography, Gauld, Colin 2004 Science & Education, issue 7, volume 13, 811-832 (http://dx.doi.org/10.1007/s11191-004-9508-7)
- ↑ The exact equation of motion of a simple pendulum of arbitrary amplitude: a hypergeometric approach, M I Qureshi et al 2010 Eur. J. Phys. 31 1485(http://dx.doi.org/10.1088/0143-0807/31/6/014)
- ↑ A comprehensive analytical solution of the nonlinear pendulum, Karlheinz Ochs 2011 Eur. J. Phys. 32 479 (http://dx.doi.org/10.1088/0143-0807/32/2/019)