Campo de indução magnético criado por 2 condutores
Contents
Descrição da experiência
O campo de indução magnética existe em todo o espaço que nos rodeia, quer pelo magnetismo natural terrestre e sideral quer criado pelo Homem. Podemos distinguir dois tipos de categorias, (i) os campos constantes com reduzida influência nos sistemas biológicos e (ii) os variáveis no tempo (AC), capazes de induzir correntes elétricas. Estes últimos, a partir de valores elevados podem ser prejudiciais, principalmente para humanos com próteses eletrónicas (p.ex. pacemakers).
No entanto a maioria dos circuitos elétricos, incluindo as linhas de transmissão elétricas, são fechados ou seja, as correntes acabam por retornar à fonte (gerador ou bateria) por cabos muito próximos uns dos outros. É o que acontece nos nossos cabos domésticos onde os mais atentos certamente já repararam que andam sempre aos pares (o terceiro fio normalmente é a "terra" e não transporta energia, servindo apenas o propósito de proteção).
O objetivo desta experiência consiste em determinar o vetor do campo de indução magnética em vários pontos do espaço criado pelos dois condutores paralelos afastados entre si. O protocolo avançado sugere uma resolução matemática mais exigente duma bobine quadrada onde toda a geometria é tida em consideração. Para o efeito a experiência é dotada duma micro-sonda 3D que recolhe a intensidade do campo magnético nos pontos selecionados.
Se quiser fazer parte da rede MEDEA, por favor envie-nos um mail.
Ligações
- Video: rtsp://elabmc.ist.utl.pt/Mag3D.sdp
- Laboratório: Intermédio em e-lab.ist.eu
- Sala de controlo: Mag_3D
- Nível: **
Quem gosta desta iniciativa
Aparato experimental
Esta experiência consiste em dois cabos paralelos de cobre por onde passa uma corrente elétrica geradora dum campo de indução magnético. O fluxo magnético gerado pelo campo é detetado numa micro-sonda de três eixos (pick-up coil) que permite reconstruir num plano préviamente selecionado a geometria vetorial magnética. Por razões práticas o plano onde são recolhidos os dados encontra-se 10 mm abaixo do eixo de rotação da bobine.
A corrente tem de ser fechada nos extremos pelo que a implementação real consiste numa bobine retangular onde um dos lados é subtancialmente maior do que os extremos.
| Lado menor (2a) | 89mm +/- 0.5mm |
| Lado maior (2b) | 454mm +/- 0.5mm |
| Numero de espiras | 20, (AWG 24) |
A micro-sonda é constituída por três bobinas quadrangulares enroladas sobre um torreão cúbico de PVC com 5mm de lado e 10 espiras cada. Cada uma destas espiras encontra-se orientada segundo 3 eixos ortogonais, sendo o sinal do campo magnético detectado e amplificado adequadamente por eletrónica concebida para o efeito (filtro sintonizado). No final determina-se a medida do fluxo magnético nesse pequeno volume segunda cada eixo. Refira-se que é usada uma excitação alternada da corrente (AC-30kHz) para se poder desprezar a contribuição do campo magnético terrestre e outros campos espúrios e não sendo utilizado nenhum metal nas proximidades que possa alterar a configuração do campo.
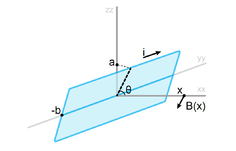
A experiência permite configurar o ângulo do observador com o plano dos cabos mais compridos e varrer radialmente segundo o eixo dos xx a distância a estes. Efetuando vários varrimentos é possível mapear a área em torno dos cabos. Um ângulo de 0º corresponde a posicionar a bobine na vertical (orientada segundo os eixo dos zz) criando um campo maioritáriamente segundo os zz e a 90º esta fica orientada no eixo dos xx. Na prática é a bobine rodada no eixo dos yy, sendo o deslocamento da micro-sonda sempre segundo o eixo dos xx.
Orientação duma bobine
A definição da orientação duma bobine prende-se com o campo de indução gerado por esta segundo a regra da mão direita: assim adoptamos a definição de que uma bobine está alinhada na vertical ─ eixos dos zz ─ caso as suas espiras estejam bobinadas no plano xx-yy.
Realça-se novamente que a micro-sonda desloca-se ligeiramente abaixo (10 mm) do plano médio definido pelos condutores para poder passar por estes ao ser efetuado o varrimento. Este facto tem grande importância no protocolo avançado na zona próxima aos condutores embora não seja relevante para o cálculo do campo longínquo.
MEDEA
Esta experiência é utilizada no projeto MEDEA, uma parceria entre a SPF e REN, Redes Energéticas Nacionais. MEDEA É O acrónimo para designar a MEDição dos campos Electromagnéticos no Ambiente, realizado por alunos de várias escolas secundárias e profissionais e que visa medir o campo eléctrico e magnético no meio ambiente.
Física
A determinação do campo de indução magnético implica integrar a lei de Biot-Savart segundo o percurso da bobine, somando num ponto do espaço todas estas contribuições infinitésimais de uma forma vectorial. No entanto a geometria foi seleccionada de forma a permitir usar um formalismo mais simples baseado na contribuição para o campo gerado por condutores infinitos.
Campo gerado por dois cabos infinitos
No plano onde coexistem ambos os cabos
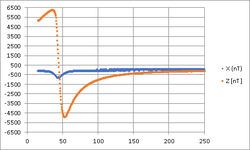
[File:MAG_3D_MagneticField_90degree.png|250px|thumb|right| Componentes segundo os zz e xx para o campo criado pela experiência com a espira alinhada no eixo dos xx]]
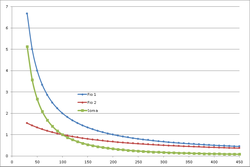
Se considerarmos dois condutores de diâmetro desprezável separados por uma distancia d=2a onde o segundo é percorrido pela corrente de retorno do primeiro cabo, apesar do decaímento do campo de indução magnético de um condutor individual depender do inverso da distância (~1/r), ao considerarmos o efeito dos dois em conjunto esse decaímento é muito mais abrupto ficando com uma dependência do inverso do quadrado da distância em zonas distantes.
Isso mesmo pode ser verificado através da expressão simplificada obtida a partir da lei de Gauss e calculada no plano onde existem os dois condutores:
[math] B_{Total}=B_1+B_2=\frac{\mu _0 i}{2 \pi (r-a)}- \frac{\mu _0 i}{2 \pi (r+a)}\simeq \frac{\mu _0 i a}{\pi r^2}, r\gg d [/math]
onde
[math] \frac{\mu _0 i}{2 \pi r} [/math] representa o módulo do campo de indução magnético criado por um condutor linear infinito.
Os valores experimentais obtidos encontram-se na figura seguinte onde se mostram apenas as duas dimensões relevantes (segundo yy o campo é despresável por uma questão de simetria).
No plano de simetria entre os cabos
Nesta situação, o àngulo da bobine com o eixo dos 'xx é nulo e por uma questão de simetria, só existe campo segundo xx nesse eixo ortogonal ao plano definido pelos cabos. Numa região afastada podemos considerar que a distância r ao plano, dada por [math]\sqrt{a^2+x^2}[/math] é próxima da sua ordenada no eixo e ambos os cabos ─ afastados entre si de 2a ─ concorrem para gerarem um campo construtivo com o dobro da intensidade pelo que:
[math] B_{Total}=B_1+B_2 \approx 2 \times \frac{\mu _0 i}{2 \pi \sqrt{a^2+x^2}} \cdot \frac{a}{\sqrt{a^2+x^2}} = \frac{\mu _0 i a}{\pi (a^2+x^2)} [/math]
e para [math] x \gg a [/math] simplifica para:
[math] B_{eixo}= \frac{\mu _0 i a}{\pi x^2} , x \approx r\gg a [/math]
Campo gerado por uma bobine retangular
O estudo generalizado da geometria retangular implica o cálculo do campo de indução magnético através da integração da contribuição dos elementos infinitesimais da corrente sobre a espira cuja contribuição é:
[math] d{\bf{B}} = \frac{{\mu _0 }}{{4\pi }}\frac{{Id\ell \times {\bf{\hat r}}}}{{r^2 }} [/math]
Esta integração pode ser simplificada considerando que a sonda se desloca apenas segundo o eixo dos xx para z=y=0 (por razões práticas aproximamos a posição real y=-10mm≃0) e por simetria pode-se estabelecer que o campo segundo os yy é nulo.
Estudos experimentais
A orientação do campo
A visualização dum campo vetorial nem sempre é bem conseguida. Na análise deste trabalho a melhor forma de proceder é usar um software que permita visualizar os vetores do campo de indução magnética a cada 10 mm numa projeção tridimensional. Para tal sugere-se a utilização do Octave, Matemática, Pyton, IDL ou MatLab. Neste link (BiotSavart.ipynb) poderá encontrar uma simulação efetuada em Jupyter.
Linhas de campo e curvas de nível
Obtendo-se várias características fruto da seleção de ângulos diversos, consegue-se mapear numa superfície de simetria no plano xx-zz valores para o módulo do campo e a sua direção, analisando o seu comportamento espacial. As linhas de campo, que seguem os vectores espacialmente permitem identificar facilmente a orientação do fluxo magnético. As curvas de nível ligam pontos do módulo do campo constante identificando as regiões do espaço onde a sua variação é maior ou menor pelo espaçamento entre elas.
Bibliografia