Conservação do Momento Angular
Contents
Descrição da Experiência
Esta sala de controlo permite confirmar a conservação do momento angular colidindo um disco a rodar com outro inicialmente em repouso. É também possível inferir o momento de inércia através de princípios de conservação de energia.
Aparato Experimental
O aparato experimental consiste num motor de disco rígido de computador equipado com um disco de 115 gr. com raio interior 12,5mm e exterior 47,5mm. Um segundo disco com 69 gr. e as mesmas dimensões do primeiro é suspenso acima dele e pode ser largado por um servo-motor.
O motor do aparato pode ser usado como um gerador equipado com uma resistência comutável que serve de travão electromagnético e é comandada por um microcontrolador. A característica de corrente/voltagem de travagem é medida permitindo um cálculo rigoroso da dissipação de energia.
Protocolo - Conservação do Momento Angular
O disco de baixo é acelerado pelo motor até atingir uma velocidade angular seleccionada. Neste instante a alimentação do motor é desligada, o disco fica a rodar livremente e a sua velocidade de rotação vai sendo medida. Quando for atingida uma velocidade escolhida previamente, o servo deixa cair o disco suspenso inicialmente em repouso sobre o disco em rotação.
Os resultados da experiência são fornecidos e traçados graficamente com a velocidade dos discos em função do tempo.
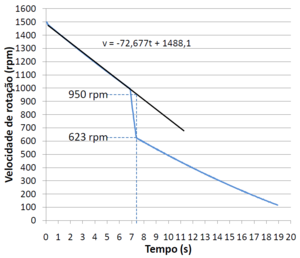
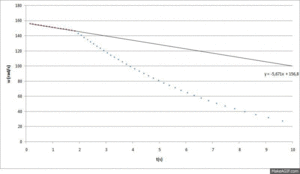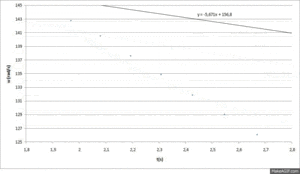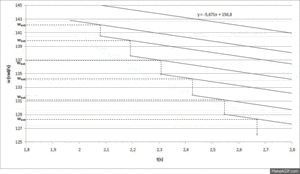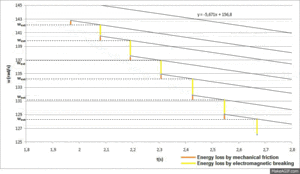
A Figura1 é um gráfico criado no Microsoft Excel a partir da tabela de resultados de uma experiência em que o servo deixa o disco suspenso cair quando o disco inferior atinge 1000 rpm.
Fazendo uma regressão linear entre o início da desaceleração e a queda dos discos, é possível extrapolar a velocidade prevista dos discos em rotação em qualquer instante.
Física
Usando as seguintes quantidades:
L - momento angular
I - momento de inércia
ω - velocidade angular
m - massa em rotação.
Tem-se para a conservação do momento angular:
$L_i=L_f$
$I_i \omega_i=I_f \omega_f$
$\frac{I_i}{I_f}=\frac{\omega_f}{\omega_i}$
$\frac{\frac{m_i\left (r_1^2+r_2^2 \right )}{2}}{\frac{m_f\left (r_1^2+r_2^2 \right )}{2}}=\frac{\omega_f}{\omega_i}$
$\frac{m_i}{m_f}=\frac{\omega_f}{\omega_i}$
Obtém-se experimentalmente
$\frac{\omega_f}{\omega_i}=\frac{623}{950}=0,656$
enquanto que pela razão das massas
$\frac{m_i}{m_f}=\frac{115}{115+69}=0,625$
Fazendo um desvio à exatidão
$\frac{\left|0,656-0,625\right|}{\left|0,625\right|}\times 100=4,9\%$
Conclui-se que a razão das velocidades (experimental) difere 4,9% da razão das massas (teórica), que está de acordo com a conservação do momento angular.
Sabendo as dimensões exatas dos discos ($r_1=12,5mm, r_2=47,5mm$) e acrescentando o momento de inércia do rotor do motor às equações, este acumula o desvio ao esperado e é possível calcular o seu valor aproximado (ou a sua massa, sabendo o seu raio).
$I_i \omega_i=I_f \omega_f$
$\left (I_m + I_{Di}\right ) \omega_i=\left (I_m + I_{Df}\right ) \omega_f$
Resolvendo em ordem a $I_m$
$I_m = \frac{I_{Df} \omega_f - I_{Di} \omega_i}{\omega_i-\omega_f}$
Protocolo Avançado - Medição do Momento de Inércia
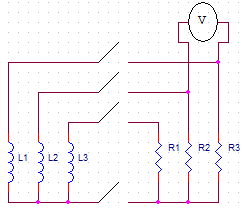
O disco de baixo é acelerado pelo motor do disco rígido até uma velocidade angular seleccionada. Neste instante a alimentação do motor é desligada e o disco fica a rodar livremente. Quando for atingida uma velocidade escolhida previamente, um relé coloca cada enrolamento do motor em paralelo com uma resistência com uma impedância igual à impedância do enrolamento (Figura 3). Estas resistências vão dissipar energia actuando como um travão electromagnético. Tensão aos terminais de uma das resistências e velocidade do disco em função do tempo são fornecidas numa tabela no final da sessão.
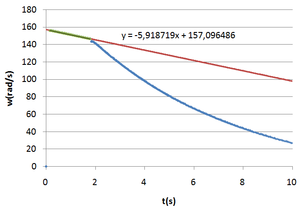
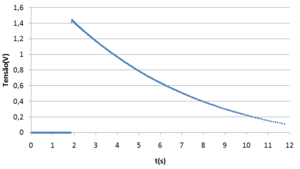
As Figuras 2 e 4 são gráficos obtidos partir da tabela de resultados de uma experiência em que o relé liga o travão electromagnético quando os discos atingem 1400 rpm.
Fazendo um ajuste aos primeiros dados da Figura 2 gerados antes de o relé ligar, obtém-se uma recta cujo declive nos fornece a desaceleração angular do disco devido ao atrito, assumida como constante. Pela desaceleração pode-se calcular diferencialmente a perda instantânea do momento angular.
Usando os dados da velocidade dos discos faz-se um balanço da energia dos discos entre cada aquisição. A perda de energia mecânica dos discos terá que ser igual à soma das perdas por atrito mecânico e por dissipação de energia nas resistências.
$\Delta E_{mec} = \Delta E_{atrito} + \Delta E_{ele}$
A energia de um corpo em rotação é $E_{rot}=\frac{Iw^2}{2}$ em que I é o momento de inércia, logo, a variação de energia mecânica entre cada aquisição será:
$\Delta E_{mec}=\frac{I(w_{2exp}^2-w_{1exp}^2)}{2}$
em que $w_{2exp}$ e $w_{1exp}$ correspondem à velocidade angular experimental do disco no instante da aquisição e no instante anterior respetivamente.
Usando o declive da reta ajustada à desaceleração inicial derivada do atrito mecânico é possível extrapolar $w$ para a aquisição seguinte se o relé não estivesse ligado. Deste modo podemos inferir a variação de energia mecânica causada pelo atrito mecânico mas:
$\Delta E_{mec}=\frac{I(w_{ext}^2-w_{exp}^2)}{2}$
em que $w_{exp}$ é a velocidade angular experimental do disco no instante da aquisição e $w_{ext}$ é a velocidade extrapolada do disco numa situação sem atrito eletromagnético no instante da próxima aquisição. Um conjunto de extrapolações de $w_{ext}$ é visível na Figura 5.
A potência dissipada no "atrito eletromagnético" corresponde a
$P=VI=\frac{V^2}{R}$
A tensão rms aos terminais de um enrolamento corresponde a
$V_{rms}=\frac{V_{medida}}{\sqrt{3}\sqrt{2}}$
Na montagem usada, a energia dissipa-se em 3 ramos o que leva a multiplicar por 3. Tanto o enrolamento como a resistência têm uma impedância de $4,7\Omega$ e por estarem em paralelo a impedância será metade, o que equivale a deixar $R=4,7\Omega$ e multiplicar por 2 a potência.
$P=3\times2\times\frac{V_{rms}^2}{R}=3\times2\times\left(\frac{V_{medida}}{\sqrt{3}\sqrt{2}}\right)^2\frac{1}{R}$
$P=\frac{V^2}{R}$
A energia dissipada será:
$\Delta E_{ele}=P*\Delta t$
Em que $\Delta t$ é o tempo entre aquisições.
O balanço da energia é feito para cada par de aquisições consecutivas e no final somado:
$Balanço = \Delta E_{mec} - \Delta E_{atrito} - \Delta E_{ele}$
Finalmente usa-se a função "goal-seek" do Microsoft Excel para colocar o somatório dos balanços a 0 (zero) iterando o valor do momento de inércia (I).
Usando este método, consegue-se inferir um valor experimental de $1,52\times10^{-4}$ $kg$ $m^2$ para o momento de inércia.
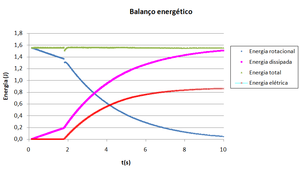
A Figura 6 ilustra a energia dos discos ao longo do tempo, a energia perdida por atrito e pela travagem eletromagnética e a soma de todas as energias permitindo verificar a conservação de energia ao longo de toda a experiência.
Ora, os discos desta experiência são na verdade coroas circulares de raios interior 12,5mm e exterior 47,5mm. O seu momento de inércia teórico corresponde então a:
$I=\frac{m\left(r_1^2+r_2^2\right)}{2}=\frac{0,115\left(0,0125^2+0,0475^2\right)}{2}=1,387\times 10^{-4}kg \; m^2$
Calculando o erro em relação ao valor esperado, obtem-se
$\frac{\left|1,525\times 10^{-4}-1,387\times 10^{-4}\right|}{\left|1,387\times 10^{-4}\right|}\times 100=10\%$
Conclui-se assim que os resultados se desviam dos calculados teoricamente por ~10%. Uma melhoria poderia ainda ser obtida incluindo um termo adicional para o momento de inércia do rotor. Caso seja efetuada a experiência com ambos os discos, poder-se-á efetuar um ajuste considerando o momento de inercia do rotor como parâmetro livre e eliminar este erro sistemático.