Difference between revisions of "Conservação do Momento Angular"
| Line 70: | Line 70: | ||
A tensão rms aos terminais de um enrolamento corresponde a | A tensão rms aos terminais de um enrolamento corresponde a | ||
| − | $V_{rms}=\frac{V_{med}{\sqrt{3}\sqrt{2}}$ | + | $V_{rms}=\frac{V_{med}}{\sqrt{3}\sqrt{2}}$ |
A potência corresponde a | A potência corresponde a | ||
Revision as of 16:18, 19 December 2012
Contents
Descrição da Experiência
Esta sala de controlo permite verificar a conservação do momento angular e medir o momento de inércia de um conjunto de discos em rotação.
Aparato Experimental
O aparato experimental consiste num disco rígido de computador ao qual foram adicionados um servo e um conjunto de discos suspensos por este. Esta montagem permite a realização do primeiro protocolo experimental, centrado no estudo da conservação do momento angular.
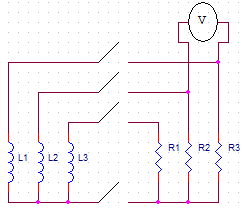
O aparato conta ainda com um conjunto de resistências de travagem que podem ser colocadas em paralelo com os enrolamentos do motor do disco por um relé. Esta montagem permite a realização do segundo protocolo experimental, centrado no estudo do momento de inércia.
Protocolo - Conservação do Momento Angular
5 discos com 115g no total são acelerados pelo motor do disco rígido até 1500rpm. Neste momento o motor desliga-se, os discos ficam a rodar livremente e a sua velocidade de rotação vai sendo adquirida. Quando for atingida uma velocidade escolhida previamente pelo utilizador, o servo deixa cair sobre os discos em rotação 3 discos com 69g no total inicialmente em repouso.
No final da sessão obtém-se uma tabela com a velocidade dos discos em função do tempo, cujos valores servirão para criar um gráfico num programa ao critério do utilizador.
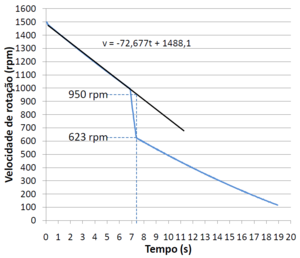
A Figura1 é um gráfico criado no Microsoft Excel a partir da tabela de resultados de uma experiência em que o servo deixa os discos suspensos cair quando os discos abaixo atingem 1000 rpm. Fazendo uma regressão entre o início da desaceleração e a queda dos discos, obtém-se uma reta cuja equação nos permite determinar a velocidade prevista dos discos em rotação no ponto em que os discos que caem deixam de deslizar sobre os que estavam em rotação.
Usando as seguintes quantidades:
L - momento angular
I - momento de inércia
ω - velocidade angular
m - massa em rotação.
Temos para a conservação do momento angular:
$L_i=L_f$
$I_i \omega_i=I_f \omega_f$
$\frac{I_i}{I_f}=\frac{\omega_f}{\omega_i}$
$\frac{\frac{m_i\left (r_1^2+r_2^2 \right )}{2}}{\frac{m_f\left (r_1^2+r_2^2 \right )}{2}}=\frac{\omega_f}{\omega_i}$
$\frac{m_i}{m_f}=\frac{\omega_f}{\omega_i}$
Obtém-se experimentalmente
$\frac{\omega_f}{\omega_i}=\frac{623}{950}=0,656$
enquanto que pela razão das massas
$\frac{m_i}{m_f}=\frac{115}{115+69}=0,625$
Fazendo um desvio à exatidão
$\frac{\left|0,656-0,625\right|}{\left|0,625\right|}\times 100=4,9\%$
Conclui-se que a razão das velocidades (experimental) difere 4,9% da razão das massas (teórica), que está de acordo com a conservação do momento angular.
Protocolo Avançado - Medição do Momento de Inércia
5 discos com 115g no total são acelerados pelo motor do disco rígido até 1500rpm. Neste momento o motor desliga-se, os discos ficam a rodar livremente e a sua velocidade de rotação e tensão entre duas fases vai sendo adquirida. Quando for atingida uma velocidade escolhida previamente pelo utilizador, um relé coloca cada enrolamento do motor em paralelo com uma resistência com uma impedância igual à impedância do enrolamento. Estas resistências vão dissipar energia actuando como um travão electromagnético.
No final da sessão obtém-se uma tabela com a velocidade dos discos e tensão entre duas fases em função do tempo, cujos valores servirão para criar gráficos num programa ao critério do utilizador.
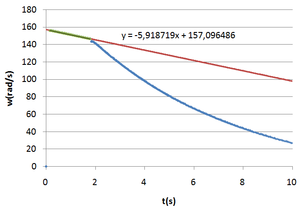
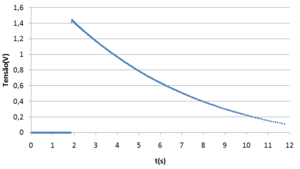
As Figuras 2 e 3 são gráficos criados no Microsoft Excel a partir da tabela de resultados de uma experiência em que o relé liga quando os discos atingem 1400 rpm.
A tensão rms aos terminais de um enrolamento corresponde a
$V_{rms}=\frac{V_{med}}{\sqrt{3}\sqrt{2}}$
A potência corresponde a
$P=VI=\frac{V^2}{R}$
Na montagem usada a energia dissipa-se em 3 ramos, no enrolamento e na resistência em paralelo, o que leva a multiplicar a potência dissipada por 3 e por 2.
$P=3*2*\frac{V_{rms}^2}{R}$
A energia de um corpo em rotação é $I=\frac{Iw^2}{2}$.
Ora, os discos desta experiência são na verdade coroas circulares de raios interior 13mm e exterior 47mm. O seu momento de inércia teórico corresponde então a:
\[I=\frac{m\left(r_1^2+r_2^2\right)}{2}=\frac{0,115\left(0,013^2+0,047^2\right)}{2}=1,367\times 10^{-4}kg \; m^2\]
Fazendo um desvio à exactidão,
\[\frac{\left|1,354\times 10^{-4}-1,367\times 10^{-4}\right|}{\left|1,367\times 10^{-4}\right|}\times 100=0,9\%\]
Conclui-se que esta experiência produziu resultados que se desviam dos calculados teoricamente por apenas 0,9%!!