Quantum interpretation of three polarizers

If we run the experiment for at least 90º of rotation is clear that we can expect a probability for a photon to pass a polarizer proportional to a sinusoidal function as in the orthogonal state no photon can pass. By the contrary in an aligned stat the probability to pass is 100%.

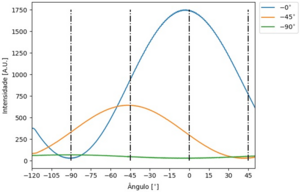
If we conduct the Polaroid experiment by doing a 180° scan, we will observe that the photons' probability of passage/transmission is proportional to a sinusoidal function, like a [math] sin^2(\theta)[/math]. The sinus has to be squared as any probability can't be negative. Note that [math] sin^2(\theta)[/math] is still a sinusoidal function.

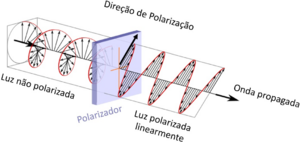
Let's describe the polarization state of light as a two-dimensional vector, as illustrated in the figure. Vertically polarized light corresponds to a vector pointing upwards (0, 1), horizontally corresponds to (1,0). We use Dirac notation to represent these vectors, |V> and |H> respectively. An arbitrary vector can be written as \(|α〉=cos⁡(α) |V〉+ sin(⁡α) |H〉 \).

Quantum mechanics explains how to calculate:

1. the probability of transmission of these states through a polarizer;
2. the state at the exit of the polarizer. When the state \(|V>\) passes through the second polarizer, oriented for instance at 45°, we have that the transmission probability is given by

[math] 〖Prob=|〈V|P_{(45°)} |V〉|〗^2=1/2 [/math]

Classical interpretation of light polarization. This interpretation is only possible for a immense number of photons, for a single or few ones we need to assume a quantize state associated with each photon.

In the case of several polarizers with a small incremental angle until the final one at 90º it can be showed that the probability for the photon to pass the cascade of polarizers became increasingly greater becoming 100% for an infinite number of polarizers!

So, the photon behavior through a polarizer can be interpreted as:

1. Initial Polarization State: A photon approaching a polarizer has a specific polarization state, which can be represented as a superposition of the two basis states defined by the polarizer's axis, (i) paralleled aligned or vertical state and (ii) orthogonal or horizontal state.
2. Interaction with the Polarizer: Upon encountering the polarizer, the photon's polarization state is measured relative to the polarizer's axis. This process projects the photon's polarization onto one of two orthogonal components: (i) Parallel to the polarizer axis (transmitted) or (ii) Perpendicular to the polarizer axis (absorbed or blocked). The probability of the photon transmission is given by \(P_{transmit}=cos^{⁡2}(\theta)\), where θ is the angle giving the probability between the two states which in the classical theory resumes to the angle with the polarizer's axis.
3. Post-Polarization State: If the photon passes through, according to the probability, its polarization state is now aligned with the polarizer axis that it just pass by (it no longer retains its original polarization state, being this a key distinction from classical theory).

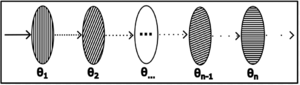
Now if we have a chain of polarizers, ie if multiple polarizers are placed in sequence, with each successive polarizer rotated by a small angle Δθ, the total probability of a photon passing through all N polarizers is:

[math] P_{total}=\prod_{i=1}^{N−1} cos^{⁡2}(Δθ) [/math]

where \(Δθ=\frac{90º}{(N−1)}\)

This simplifies to:

[math] P_{total}=(cos^{⁡2}(Δθ))^{N−1} [/math]

Example:

Suppose N=10 polarizers are used to go from θ=0º to θ=90º. Then, \( Δθ=90º/9=10º\).

• Probability of passing each step: \( P_i=cos⁡^{2}(10º)≈0,97 \).
• Total probability: \(P_{total}​=(0.9698)^9≈0.75\)

This result shows that gradual rotation increases the probability of transmission compared to using just two polarizers oriented at 0º and 90º directly, where no photons would pass at all as \(cos^{⁡2}(90º)=0\).

Key Points of Clarification:

• The photon does not keep its original polarization if it passes through; rather, it becomes aligned with the polarizer axis.
• The outcome is probabilistic: a photon may or may not pass a polarizer, based on the projection of its initial polarization onto the polarizer's axis.
• This phenomenon underscores the quantum mechanical principles of state collapse and measurement, distinct from classical wave explanations.