Difference between revisions of "Quantum interpretation of three polarizers"
| Line 1: | Line 1: | ||
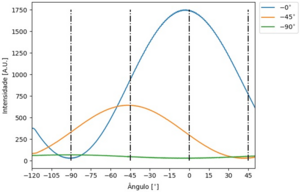
| + | If we conduct the "Polaroide" experiment by doing a scan, lets say, of 180º rotation, we will conclude that the photons probability should be proportional to a sinusoidal function, like a <math> sin^2(\theta)</math>. The sinus has to be squared as any probability can't be negative. Note that <math> sin^2(\theta)</math> is still a sinusoidal function. | ||
| + | |||
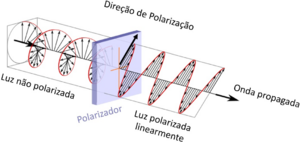
Let's describe the polarization state of light as a two-dimensional vector, as illustrated in the figure. Vertically polarized light corresponds to a vector pointing upwards (0, 1), horizontally corresponds to (1,0). We use Dirac notation to represent these vectors, |V> and |H> respectively. An arbitrary vector is written as \(|α〉=cosα |V〉+sinα |H〉 \). | Let's describe the polarization state of light as a two-dimensional vector, as illustrated in the figure. Vertically polarized light corresponds to a vector pointing upwards (0, 1), horizontally corresponds to (1,0). We use Dirac notation to represent these vectors, |V> and |H> respectively. An arbitrary vector is written as \(|α〉=cosα |V〉+sinα |H〉 \). | ||
Revision as of 09:50, 25 December 2024
If we conduct the "Polaroide" experiment by doing a scan, lets say, of 180º rotation, we will conclude that the photons probability should be proportional to a sinusoidal function, like a [math] sin^2(\theta)[/math]. The sinus has to be squared as any probability can't be negative. Note that [math] sin^2(\theta)[/math] is still a sinusoidal function.
Let's describe the polarization state of light as a two-dimensional vector, as illustrated in the figure. Vertically polarized light corresponds to a vector pointing upwards (0, 1), horizontally corresponds to (1,0). We use Dirac notation to represent these vectors, |V> and |H> respectively. An arbitrary vector is written as \(|α〉=cosα |V〉+sinα |H〉 \).
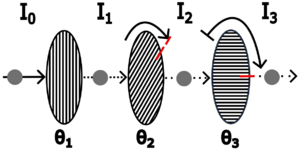
Quantum mechanics explains how to calculate: 1) the probability of transmission of these states through a polarizer, 2) the state at the exit of the polarizer. When the state \(|V>\) passes through the second polarizer, oriented at 45°, we have that: The transmission probability is given by
[math] 〖Prob=|〈V|P_(45°) |V〉|〗^2=1/2 [/math]