Difference between revisions of "Sonda de Langmuir"
| Line 69: | Line 69: | ||
Usando os valores tabelados para a área da sonda e a velocidade do som dos iões do plasma, pode-se determinar a densidade electrónica do plasma. | Usando os valores tabelados para a área da sonda e a velocidade do som dos iões do plasma, pode-se determinar a densidade electrónica do plasma. | ||
| − | Visto que \(c_s = \sqrt{\dfrac{k T_e}{M}}\), e que a sonda tem \(10 mm \) de altura e um diâmetro de \(0.2 mm \), | + | Visto que \(c_s = \sqrt{\dfrac{k T_e}{M}}\), e que a sonda tem \(10 mm \) de altura e um diâmetro de \(0.2 mm \), é possível recorrer a \(i^+_{sat}\) para determinar a densidade. |
=Ligações= | =Ligações= | ||
*[[Langmuir Probe | Versão em Inglês (English Version)]] | *[[Langmuir Probe | Versão em Inglês (English Version)]] | ||
Revision as of 23:35, 17 May 2021
EM CONSTRUÇÃO
Contents
Descrição da Experiência
Os plasmas têm características diferentes de outros estados da matéria pelo que muitas ferramentas de diagnóstico foram desenvolvidas a fim de as medir. Esta experiência permite determinar algumas destas características através de um dos métodos mais simples, uma sonda eléctrica, a sonda de Langmuir. Esta é constituída por um filamento fino feito de um material condutor que é colocado no interior do plasma e que atrai ou repele os electrões do plasma de acordo com a sua polarização. A partir da análise da característica eléctrica da sonda, que é a relação entre a tensão de polarização e da respectiva corrente colectada, é possível determinar a temperatura dos electrões e a densidade do plasma.
|
Ligações
|
Videos |
Aparato Experimental
A câmara de vácuo é composta por um cilindro de pirex na qual uma descarga de luminescência é produzida por radiofrequência. Um filamento de tungsténio, com um diâmetro de 0.2 mm, é colocado no meio da câmara e parcialmente isolado por uma camada de alumina deixando somente uma ponta 10 mm exposta ao plasma a actuar como uma sonda de Langmuir. Este filamento central tem uma referência de terra em torno da sonda com cerca de 200mm, de modo a ser muito maior do que a própria sonda.
O gerador de radiofrequência (3.5W, 50kHz, 1 kV), que ioniza o gás e gera o plasma, é ligado a duas placas de molibdénio paralelas semelhantes às de um condensador.
Protocolo
Determinação da temperatura e densidade electrónica
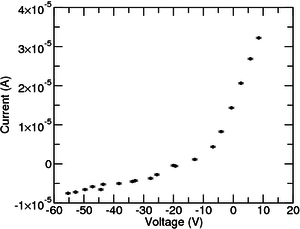
A sonda de Langmuir utiliza um ou mais eléctrodos colocados no interior do plasma para medir a corrente colectada durante a aplicação de uma tensão de polarização. Isto irá fornecer a característica IV do plasma. Normalmente é usado um sinal triangular ou dente de serra para obter pontos equiseparados.
Quando a sonda está isolada electricamente, forma-se uma bainha eléctrica na região de interface entre o plasma e a sonda. Para compensar a maior mobilidade dos electrões, a sonda vai atingir um potencial flutuante, \(V_f\), negativo em relação ao potencial de plasma, \(V_p\). A densidade na entrada da bainha é de, aproximadamente, metade da densidade quando longe da sonda (critério de Bohm).
A tensão de sonda em relação ao enrolamento de referência, \(V_s\), é varrida utilizando uma fonte de tensão variável. Se a polarização da sonda, comparando com o potencial do plasma, for bastante negativa, todos os electrões serão repelidos e o fluxo de iões para a sonda é independente do potencial aplicado. Num plasma totalmente ionizado, esta corrente de saturação de iões é descrita pela seguinte fórmula: [math] i^+_{sat} = j^+_{sat} A_s = \frac{e \, n \, c_s \, A_s}{2} [/math]
Em que \(j^+_{sat}\) é a densidade de corrente iónica, \(A_s\) a superfície de contato da sonda, \(e \) a carga do electrão, \(n\) a densidade iónica da plasma e \(c_s\) a velocidade do som dos iões.
Quando a tensão de polarização aplicada à sonda aumenta, a queda de potencial na bainha é reduzida e os electrões serão capazes de alcançar a sonda. Assumindo uma distribuição de Maxwell para a velocidade dos electrões, a relação entre corrente e tensão será: [math] i = -i^+_{sat} \left( 1- e^{\dfrac{e}{k T_e} (V_s - V_f)} \right) [/math]
Em que \(T_e\) é a temperatura electrónica. Esta expressão assume também que há apenas uma sonda e que esta é nao perturbativa.
A partir da última equação é possível extrair uma estimativa do potencial flutuante, \(V_f \). Isto é feito tomando o valor no qual a característica cruza o zero.
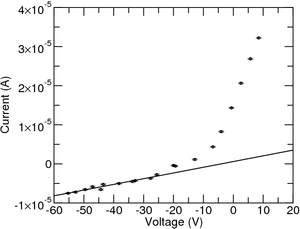
Também se verifica facilmente que os dados não acompanham a característica do lado da saturação iónica, que devia ser constante em vez de ter um declive. Isto tem que ver com o facto da largura da bainha aumentar com a tensão aplicada. Para corrigir isto, ajusta-se uma função linear desse lado e de seguida subtrai-se o declive desta (como pode ser visto na Figura 3). Alternativamente, pode-se incluir essa contribuição na equação: [math] i = -i^+_{sat} \left( 1- \alpha\ (V_s-V_f) - e^{\dfrac{e}{k T_e} (V_s - V_f)} \right) [/math]
No entanto, sendo que se pretende obter a densidade, é necessário fazer uma outra correção que corresponde à soma do valor da corrente no ponto em que esta é completamente devida aos iões, ou seja, para valores de tensão muito menores do que o potencial flutuante (tipicamente usa-se duas vezes o potencial flutuante, daí a necessidade da estimativa inicial).
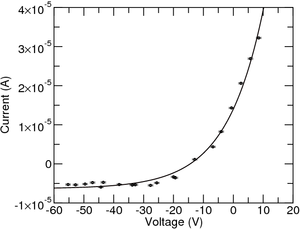
Depois disso, os dados experimentais têm de ser ajustados à equação apresentada anteriormente (como se vê na Figura 4). A partir do ajuste \(T_e \), pode ser extraída, tanto a corrente de saturação iónica, \(i^+_{sat}\), como o potencial flutuante \(V_f \). Este útlimo deve ter um valor próximo daquele que foi determinado empiricamente.
Usando os valores tabelados para a área da sonda e a velocidade do som dos iões do plasma, pode-se determinar a densidade electrónica do plasma. Visto que \(c_s = \sqrt{\dfrac{k T_e}{M}}\), e que a sonda tem \(10 mm \) de altura e um diâmetro de \(0.2 mm \), é possível recorrer a \(i^+_{sat}\) para determinar a densidade.